Zeros of the Quadratic

We’ve seen how vertex form and intelligent use of the axis of symmetry can help to draw
an accurate graph of the quadratic function defined by the equation f(x) = ax²+bx+c.
When drawing the graph of the parabola it is helpful to know where the graph of the
parabola crosses the x-axis. That is the primary goal of this section, to find the zero
crossings or x-intercepts of the parabola.

Before we begin, you’ll need to review the techniques that will enable you to factor
the quadratic expression ax² + bx + c.

Factoring ax² + bx + c when a = 1

Our intent in this section is to provide a quick review of techniques used to factor
quadratic trinomials. We begin by showing how to factor trinomials having the form
ax² + bx + c, where the leading coefficient is a = 1; that is, trinomials having the form
x²+bx+c. In the next section, we will address the technique used to factor ax²+bx+c
when a ≠ 1.

Let’s begin with an example.

Example 1. Factor x² + 16x − 36.

Note that the leading coefficient, the coefficient of x², is a 1. This is an important
observation, because the technique presented here will not work when the leading
coefficient does not equal 1.

Note the constant term of the trinomial x² +16x−36 is −36. List all integer pairs
whose product equals −36.

Note that we’ve framed the pair −2, 18. We’ve done this because the sum of this
pair of integers equals the coefficient of x in the trinomial expression x² + 16x − 36.
Use this framed pair to factor the trinomial.

x² + 16x − 36 = (x − 2)(x + 18)

It is important that you check your result. Use the distributive property to multiply.

(x − 2)(x + 18) = x(x + 18) − 2(x + 18)
= x² + 18x − 2x − 36
= x² + 16x − 36

Thus, our factorization is correct.

Let’s summarize the technique.

Let’s look at another example.

Example 2. Factor the trinomial x² − 25x − 84.

List all the integer pairs whose product is −84.

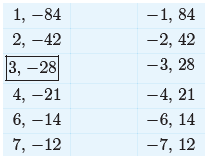
We’ve framed the pair whose sum equals the coefficient of x, namely −25. Use this
pair to factor the trinomial.

x² − 25x − 84 = (x + 3)(x − 28)

Check.

(x + 3)(x − 28) = x(x − 28) + 3(x − 28)
= x² − 28x + 3x − 84
= x² − 25x − 84

With experience, there are a number of ideas that will quicken the process.

• As you are listing the integer pairs, should you happen to note that the current
pair has the appropriate sum, there is no need to list the remaining integer pairs.
Simply halt the process of listing the integer pairs and use the current pair to factor
the trinomial.

• Some students are perfectly happy being asked “Can you think of an integer pair
whose product is c and whose sum is b (where b and c refer to the coefficients of
x²+bx+c)?” If you can pick the pair “out of the air” like this, all is well and good.

Use the integer pair to factor the trinomial and don’t bother listing any integer
pairs.

Now, let’s investigate how to proceed when the leading coefficient is not 1.

Factoring ax² + bx + c when a ≠ 1

When a ≠ 1, we use a technique called the ac-test to factor the trinomial ax² +bx+c.
The process is best explained with an example.

Example 3. Factor 2x² + 13x − 24.

Note that the leading coefficient does not equal 1. Indeed, the coefficient of x² in
this example is a 2. Therefore, the technique of the previous examples will not work.
Thus, we turn to a similar technique called the ac-test.

First, compare

2x² + 13x − 24 and ax² + bx + c

and note that a = 2, b = 13, and c = −24. Compute the product of a and c. This is
how the technique earns its name “ac-test.”

ac = (2)(−24) = −48

List all integer pairs whose product is ac = −48.

We’ve framed the pair whose sum is b = 13. The next step is to rewrite the trinomial
2x² + 13x − 24, splitting the middle term into a sum, using our framed integer pair.

2x² + 13x − 24 = 2x² − 3x + 16x − 24

We factor an x out of the first two terms, then an 8 out of the last two terms. This
process is called factoring by grouping.

2x² − 3x + 16x − 24 = x(2x − 3) + 8(2x − 3)

We now factor out a common factor of 2x − 3.

x(2x − 3) + 8(2x − 3) = (x + 8)(2x − 3)

It’s helpful to see the complete process as a coherent unit.

2x² + 13x − 24 = 2x² − 3x + 16x − 24
= x(2x − 3) + 8(2x − 3)
= (x + 8)(2x − 3)

Check. Again, it is important to check the answer by multiplication.

(x + 8)(2x − 3) = x(2x − 3) + 8(2x − 3)
= 2x² − 3x + 16x − 24
= 2x² + 13x − 24

Because this is the original trinomial, our solution checks.

Let’s summarize this process.

Let’s look at another example.