Math 200a Fall 2008 Exam 1

1. Let G be the group given by the presentation

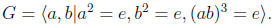
Prove that G is isomorphic to a very familiar finite group.

2. The category of politically colored sets C is defined as follows. An
object of C is a pair (X, f), where X is a set and f : X → {blue, red} is
a function. (Intuitively, you should think of f as a fixed coloring of the
elements of X with the colors red and blue.) The set of morphisms from
(X, f) to (Y, g) consists of all functions 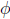: X → Y which preserve color,
in other words such that 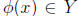  has the same color as x ∈ X for all x.
Composition of morphisms is composition of functions. It is easy to see this
satisfies the definition of a category, do not prove this.

First recall the definition of the product of two objects in the category
C. Then show by explicit construction that the product of any two objects
exists in this category. (Do this only for two objects as suggested, not an
arbitrary family.)

3. Let n be an integer with n ≥5. Show that S_n has exactly one proper
normal subgroup, freely using any results about permutation groups from
the book or from class.
(Hint: what is special about A_n for n ≥5? Use this fact in your proof.)

4. Let G be a finitely generated group. Show that as long as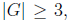
then the automorphism group of G, Aut G, contains at least two elements.

Math 200a Final, 12/9/2008

You do not have to do all problems to get a good score. I prefer complete and
correct solutions to fewer problems than sketchy solutions to more problems.
However, don't aim for perfection in your write-ups at the expense of not
doing problems which you are able to do. You may quote results proved
in class or in the textbook, but try to avoid quoting results proved only in
homework exercises.

1. In this problem, you will study (part of) the classsification of groups
of order 12 in terms of semidirect products (Hungerford classified groups of
order 12 by a more ad-hoc method.)

1a. Suppose that l G l = 12 and G does not have a normal Sylow 3-
subgroup. Show that 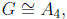, the alternating group on four symbols. (Hint:
study an action of G on something.)

1b. Suppose that l G l = 12 and G has a normal Sylow 3-subgroup. Show
that G is isomorphic to a semidirect product 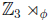H for some group H of
order 4 and homomorphism 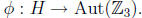Describe all of the possibilities
for H and .

1c. Prove carefully that one of the semidirect products you found in part
(b) is isomorphic to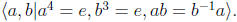

2. A group G is called polycyclic if it has a subnormal series

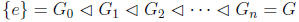
(so G_i is normal in G_i+1, but not necessarily normal in the whole group G),
such that 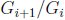is a cyclic group ( finite or infinite) for all 0≤ i < n.

2a. Show that subgroups and factor groups of polycyclic groups are again
polycyclic.

2b. Show that a finite group G is polycyclic if and only if it is solvable.

2c. Give an example, with proof, of an in finite group G which is solvable
but not polycyclic.

3. Find, with proof, the smallest odd positive integer n such that there
exists a group G of order n which is not nilpotent.

4a. Let C be a concrete category. Suppose A is an object of the category
and 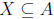is a subset. Define what it means for A to be free on the subset
X.

4b. Let C be the category whose objects are all rings (with identity),
whose morphisms are all ring homomorphisms which are unital, i.e. send
the identity to the identity, and where composition of morphisms is just the
usual composition of functions. You do not need to prove that C is a category.
Show that the ring Z[x] is a free object in this category on the subset {x}.

5a. Let M be a left module over any ring R. Recall that for m ∈ M,
the annihilator of m is 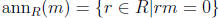, and that M is a torsion
module if 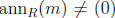   for all m in M. Now we define the annihilator of
M to be 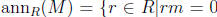  for all 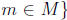. (In other words, this
is the set of ring elements that kill all elements of M.) Show that
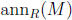
is an ideal (i.e. both left and right ideal) of R.

5b. Suppose that M is a finitely generated left module over a PID R.
State what the fundamental structure theorem for such modules (invariant
factor form) tells you about M. Show that 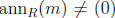  if and only if M
is a torsion module. In case 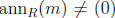, find a formula for 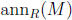in
terms of the invariant factors of M.

5c. Find an example, with proof, of a PID R and a left module M over R
such that M is not finitely generated, with the property that
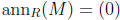
but M is nonetheless a torsion module.

6. Let Mat₂(C) be the ring of 2×2 matrices over the complex numbers.
Let S be the set of all A ∈ Mat₂(C) which satisfy the additional properties
that (i) A is invertible (i.e. detA ≠ 0), and (ii) A² is similar to A.

Show that S is equal to the union of exactly three distinct similarity
classes of matrices. (Hint: think about the Jordan canonical form.)