Rational Expression
Textbook sections and practice problems
6.1: 61–71 odd
6.3: 7-23 odd, 33-39 odd, 43-49 odd
Division of rational expressions
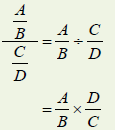
assuming B ≠ 0 , C ≠ 0 , and D ≠ 0
Example 1
Completely simplify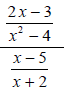
.
Verify the simplified formula for x =1.
Example 2
Completely simplify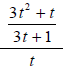
.
Verify the simplified formula for t = 2 .
Example 3
Completely simplify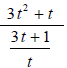
.
Verify the simplified formula for t = 2 .
Complex Fractions
A complex fraction is any fraction whose numerator or denominator contains another fraction.
Simplifying complex rational expressions – Strategy A
1. Simplify (add and/or subtract, as necessary) the expressions in the numerator
and
denominator.
2. Reciprocate the expression in the denominator and multiply with the
expression in the
numerator.
3. Simplify the remaining expression.
Example 4
Completely simplify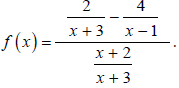 
Verify
the simplified formula for x = −1.
Example 5
Completely simplify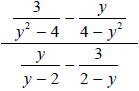 
.
Verify the simplified formula for y = 3 .
Simplifying complex rational expressions – Strategy B
1. Determine the LCD of all of the expressions in the fraction regardless of
whether the
expressions occur in the numerator or denominator.
2. Multiply along the main fraction bar by the LCD determined in step 1.
Remember to
distribute the LCD through both the numerator and denominator.
3. Simplify each product.
4. If you correctly applied steps 1 – 3, the expression is no longer a complex
rational
expression; simplify the remaining expression.
Example 6
Completely simplify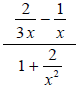 
.
Verify your formula when x = 2 and y = 1.
Example 7
Completely simplify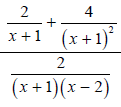 
.
Verify your formula when x = 1.
Example 8
Completely simplify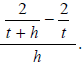 
Verify
your result using t = 1 and h = 2 .
Example 9
Completely simplify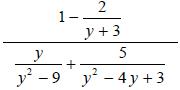 
Verify
your result when y = 2.
