The Product Rule and Power Rules for Exponents
1. Recall: An exponential expression has the form:
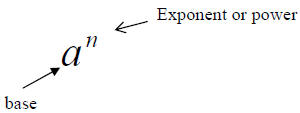
2. Usually we don’t write a power of one. That is a1
= a .
Also note that 1n =1 for any integer n.
3. This means: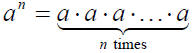
4. Be careful with negative signs.

5. Product Rule for Exponents: For any positive
integers m and n,
am · an = am+n .
Multiply like bases by adding the exponents.
If the base numbers are the same for each original factor, then the
result also has this same base. (Don’t multiply the base numbers.)
6. Power Rule (a) for Exponents: For any positive integers m and n
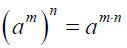 .
.
Raise a power to a power by multiplying the exponents.
7. Power Rule (b) for Exponents: For any positive integer m
(ab)m = ambm .
Raise a product to a power by raising each factor to the
power.
(This rule works for products but not for sums or differences.)
8. Power Rule (c) for Exponents: For any positive integer m
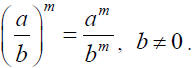
Raise a quotient to a power by raising both numerator and
denominator to the power.
9. Note the summary on page 260.
10. Often these rules are combined.

