2.1 - Matrix Operations
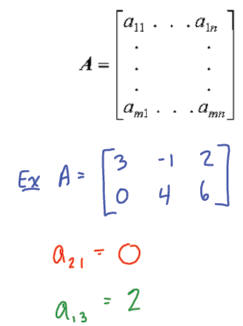
•Denoting a general matrix A of m rows and n columns
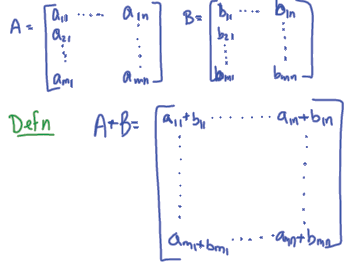
Adding matrices, multiplying by scalars
Example:

•So matrix addition and scalar multiplication are component‐wise.
•Exercise: Write a sum of two general matrices A, B
Properties of Addition & Scalar Mult
• If A, B, C are the same size, r, s any scalars,
then
• A+ B=B+ A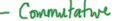
• (A+ B) +C=A+ (B+C)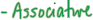
• A+0=A if 0 is the matrix of the same size, consisting
of all 0’s
•Other facts on p 108, Th 1
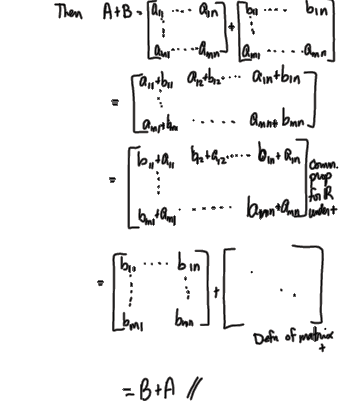
How to write a proof of a matrix fact
•Commutative property (A+ B=B+ A)
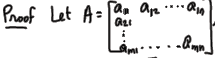
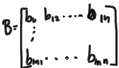
Matrix Multiplication
• We have already seen when we can multiply AB.
• Review how it works
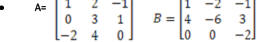
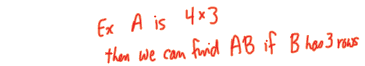
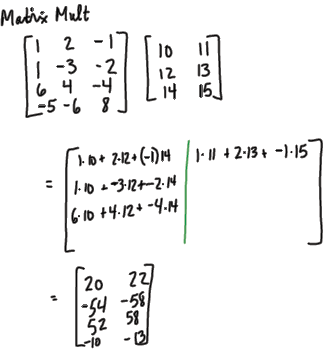
Matrix Multiplication – General Case
•Use the columns of B
(In text)
•General rule (without columns) – p 111
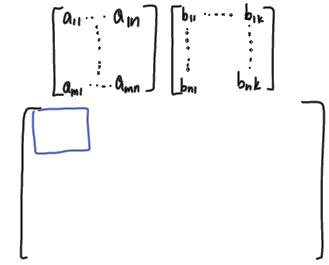
Computing a specific row/column of a product
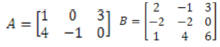
· Find
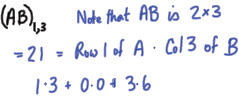
Properties of Matrix Multiplication
•P 113, Th 2
•Associative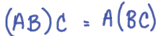
•Left Distributive
•Right Distributive
•Scalar multiples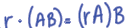
• Identity
•Note what’s missing! Verify.

Transpose AT
• Definition
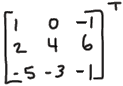
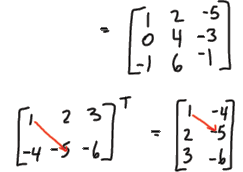
Properties of AT
•Page 115 (Th 3)