Section 5-3: Factoring Trinomials of the Form1x2 ± bx ± c
Example 1
Factor
x ^2 + 2x −24 into
(x ± a ) (x ± b)
The two last terms of
(x ± last1) (x ± last2 ) must multiply to give –24 and subtract to give +2
Step 1: The only two first terms that multiply to give x^2 are x and x. Put them
in the first places in
both of the parenthesis.
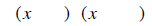
Step 2: List all the ways the last term can be multiplied to give 24.
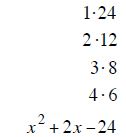
Step 3: Find the pair of products that will subtract to give + 2 (+ 6 and – 4 work)
Step 4: Put these two terms into the last places in the parenthesis. (x + 6) (x −2)
Step 5: Check your answer by FOIL.
Example 2
Factor x ^2 − 7x − 30 into (x ± a ) (x ± b)
The two last terms of (x ± last1) (x ± last2 ) must multiply to give 30 and subtract to give –7
Step 1: The only two first terms that multiply to give x^2 are x and x. Put them
in the first places in
both of the parenthesis.
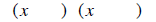
Step 2: List all the ways the last term can be multiplied to give 30.
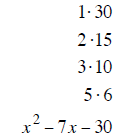
Step 3: Find the pair of products that will subtract to give - 7
(- 10 and + 3
work)
Step 4: Put these two terms into the last places in the parenthesis. (x −10) (x + 3)
Step 5: Check your answer by FOIL.
Factoring trinomials that start with a
1x^2 and end with a with a negative last term
| Example 1 | Example 2 | Example 3 |
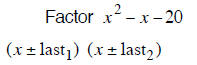 |
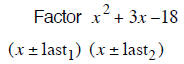 |
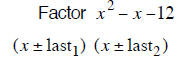 |
| last terms must multiply to 20 | last terms must multiply to 18 | last terms must multiply to 12 |
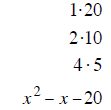 |
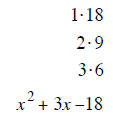 |
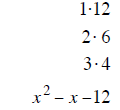 |
| last terms subtract to – 1 | last terms subtract to + 3 | last terms subtract to –1 |
| –5 and 4 subtract to – 1 | + 6 and –3 subtract to + 3 | + 3 and –4 subtract to –1 |
| (x −5) (x + 4) | (x + 6) (x − 3) | (x + 3) (x − 4) |
| Example 4 | Example 5 | Example 6 |
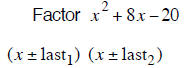 |
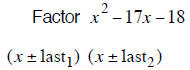 |
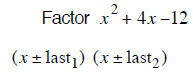 |
| last terms must multiply to 20 | last terms must multiply to 18 | last terms must multiply to 1 |
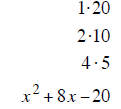 |
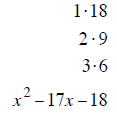 |
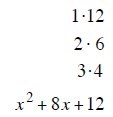 |
| last terms subtract to + 8 | last terms subtract to – 17 | last terms subtract to + 4 |
| + 10 and –2 subtract to + 8 | – 18 and + 1 subtract to – 17 | + 6 and – 2 subtract to + 4 |
| (x +10) (x − 2) | (x −1) (x −18) | (x + 6) (x − 2) |
| Example 7 | Example 8 | Example 9 |
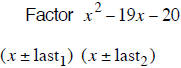 |
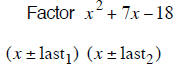 |
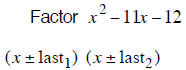 |
| last terms must multiply to 20 | last terms must multiply to 18 | last terms must multiply to 12 |
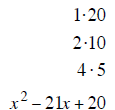 |
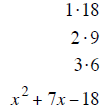 |
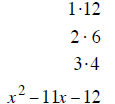 |
| last terms subtract to – 19 | last terms subtract to + 7 | last terms subtract to –11 |
| – 20 and +1 subtract to – 19 | + 9 and – 2 subtract to + 7 | –12 and + 1 subtract to –11 |
| (x −20) (x +1) | (x + 9) (x − 2) | (x −12) (x +1) |
Factoring a Polynomial Completely
To factor any polynomial completely you should factor the GCF out FIRST if the
polynomial has a
GCF. If the polynomial remaining inside the parentheses is a trinomial that can
be factored then the
complete factored answer is the product of the GCF and the factored trinomial.
Factoring The Difference of Two Perfect Squares that have a GCF
1. Factor out the GCF if there is one
2. Factor the polynomial If it can be factored.
3. The final answer is the product of the GCF and the factored trinomial.
| Example 1 | Example 2 | Example 3 |
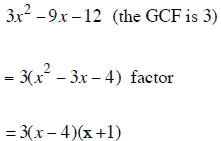 |
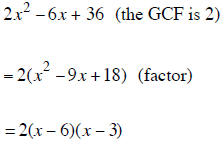 |
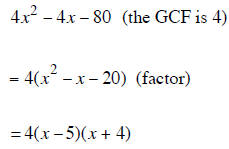 |
| The answer can be written either |
The answer can be written either |
The answer can be written either |
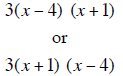 |
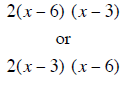 |
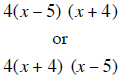 |
| Example 4 | Example 5 | Example 6 |
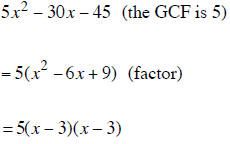 |
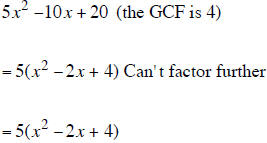 |
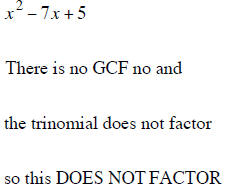 |

