Flash Cards for Factoring
Hot tips that my polynomial may be a
candidate for grouping are…
1. There is no GCF. (No factorscommon to all terms.)
2. There are 4 terms.
3. I can find a GCF if I look 2-by-2.
Priority list (steps) for factoring any
polynomial:
1. Greatest Common Factor (GCF)
2. Grouping
3. Trinomial
4. Difference of Squares
The steps for Grouping are:
1. Collect the terms into groups so that
each group has a common factor.
2. Factor out the common factor in each
group.
3. If each group now has a common
factor, factor it out. If not, regroup.
Grouping Example:
ax + bx - ay - by
= x( a + b) -y (a +b)
= ( a + b)(x - y)
Steps for factoring
ax2 + bx + c
1. Multiply the coefficient of the first term by
the last term.
2. Find factors of the product from step (1) that
add to the coefficient of the middle term. (If
none, then prime.)
3. Rename the middle term using the factors
from (2).
4. Factor by grouping.
5. Check by FOIL
Factor: 6x2 - x - 2
(Note: There isn’t enough room to show the
check on this card.)
| Prod 6(-2) = -12 | Sum -1 |
| 2(-6) = - 12 | 2 + (-6) = -4 No. |
| 3(-4) = -12 | 3 + -4 = -1 Yes. |
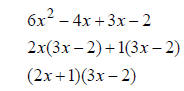
Difference of squares.
x2 - y2 = (x + y)(x - y)
Steps for solving a Polynomial Equation by
factoring.
1. Simplify and combine like terms.
Get eqn = 0.
2. Factor the polynomial.
3. Set ea. factor = 0. (zero factor prop’ty)
4. Solve ea. eqn. from step (3).
5. Check ea. sol’n in original eqn.

