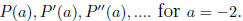Numerical Analysis
Bounds for the Roots of Polynomials: Let A = (aij) be an n * n matrix.
If Au = λu, then λ and u are called the eigenvalue and eigenvector of A,
respectively. The
eigenvalues of A are the roots of the characteristic polynomial
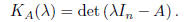
The eigenvectors are the solutions to the Homogeneous system
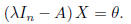
If A is symmetric, i.e., At = A, then all the eigenvalues of A are real. Let
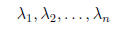
be the eigenvalues of A, then
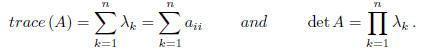
Our fist theorem is known as the Gerschgorin's Disks Theorem.
Theorem 1. Let A = (aij be an n * n matrix. For j = 1, 2, ... , n, define
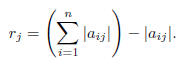
Let Dj (ajj , rj) be the
disk of radius rj with the center at the point (0, aij) of
the complex plane. Then
all the eigenvalues of the matrix A are contained within the union of the Dj
's. Thus
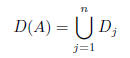
contains all the eigenvalues of A.
Remark. Since A and At have the same set
of eigenvalues, we may use Theorem 1. for
both A and At and get the best neighborhood
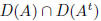for the eigenvalues of A.
Consider now the polynomial of degree n
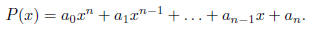
The polynomial P is said to be monic, if the leading
coefficient a0 equals one. Clearly,
the matrix
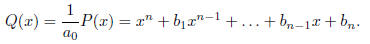
is monic. To this monic polynomial we associate an n * n matrix
The matrix CP is called the Companion Matrix of P(x).
Theorem 2. x0 is a root of p(x) if and only if x0 is an eigenvalue of the matrix CP.
Corollary. Consider a monic polynomial P(x) of degree n. Then
( i) all the roots of P(x) is contained within
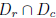, where
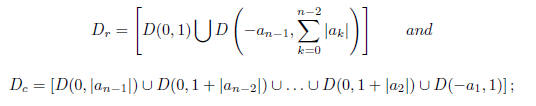
(ii) if {x1, x2, ..., xn} are the n roots of P(x), then
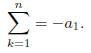
Proof. By using CP, the above theorems,
the Remark and the fact that trace(CP) = -a1,
one may readily prove the corollary.
Rational Roots: Although a real polynomial may have
complex roots, but there
is a well known theorem concerning the rational roots of polynomial with integer
coefficients.
Theorem 3. Let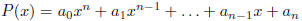 
be
a polynomial with integer coefficients.
If p/q is a rational root of P(x), then an = pr and a0 =
qs.
Nested Form: Consider the following polynomial of degree n
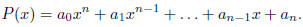
The following form of P(x) is called the nested form of P(x):
Finally, we present a root finding tool known as Horner's method or Synthetic division.
Horner's method (Synthetic Division): Consider the polynomial:
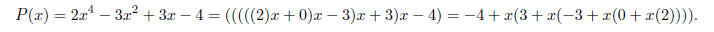
The following chart shows how to evaluate
