APPOLONIUS GASKET, FRACTALS OR HOW ADDING FRACTIONS THE WRONG WAY CAN BE INTRIGUING

There is a well-known story about a teacher who is trying hard to explain to a
student how to add fractions. After a long struggle the student understands and
the teacher feels better. Next day the student comes back to the classroom and
shows the teacher how he is adding fractions by adding both numerators to produce
the new numerator and both denominators to produce the new denominator. The
teacher is outraged and tells him: but that is not the way I explained it to you,
that is not the way to add fractions!, to which the student replied: why not? This
way is so much easier! I cannot understand why adding fractions needed to be so
complicated!”

Of course, if we do what this student wanted to do, we would not be adding
fractions of units since half a pie plus half a pie is not half a pie again (unless
someone eats half a pie when we are not looking!). But, do we need to happily
dismiss this idea just because it is not what we were looking for? Lets look a little
bit closer to what he wanted to do.

1. Adding the wrong way?

We have two fractions a/b and b/c and we combine them the following way

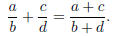
Since we agree this is not the sum of fractions, what is it? Is it the sum of
something other than fractions? You can try to guess what you are adding here,
but if you cant think of anything, wait and see.

To get a better idea lets put together the fractions one obtains when we start
with 0/1 and 1/2 , we add these two to obtain 1/3 , we add 1/2 to 1/3 to get 2/5 and so on. We
construct these fractions the way we construct Fibbonacci numbers (do you know
what Fibbonacci numbers are? Ask your mentor! it is a long story..). And here is
the first mystery you need to solve:

“If we take two consecutive fractions in your list, place the largest fraction a/b first
followed by the smallest one b/c , and do the following operation

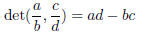
you will always get the same number. Why?”
This operation is called the determinant, and it is always found in a different
context, not that of fractions. And that is my hint to you. If you know the context
for the determinant you will know what it is that you are adding in the first place.

You then need to use a little algebra to solve the mystery. Give us a geometric
explanation of what is going on and have fun!

2. What does all this have to do with fractals, anyway?

One of the most famous fractals among mathematicians is the so-called Appolo-nius
basket. The basket is obtained the following way: We start with a disk of a
certain radius, lets choose 1/2 . We have a disk, not a circle, so think it is made of
some material. We are going to remove first three inscribed circles, all circles are
the same size and they are all tangent to each other. They touch each other, but
they do not cross through each other. It looks like this

We now look at each one of the spaces left in between the circles where we still
have some material. We take our scissors and we remove one more circle per area,
one that is also tangent to each one of the circles around it. We still have more
material left, so we remove one circle per area, one that touches, but not crosses, all
circles around. And we go on and on. Assuming you are good with your scissors,
at some point your initial circle will look like

If we had infinite time to spend doing this we would obtain a certain set left after
we remove all possible circles. Notice that this set does not have any area in it,
since, if there was any area left, you would remove a circle from it. In fact, there is
a way to define the dimension of this set as not being 1 or 2 but a fraction. What
is left only has points, lots of them! Can you show some? The set left when we
repeat this procedure to infinity (be sure to discuss with your mentor what this
phrase means!) is the Appolonius basket, a basket full of holes that is still puzzling
mathematicians!!

Our question to you about this fractal is: assume I open the circle and make its
boundary a straight line. What we have then is a straight line with circles tangent
to it, pretty much like

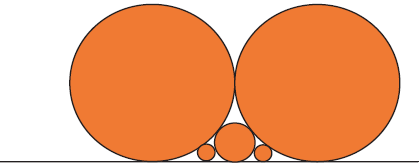
If you place one of the biggest circles at 0, can you tell us the points where the
other circles touch the line? Find out and try to explain your results. This one is
the biggest mystery in this project!

3. Some more fractals (or further suggestions for the mentors

What is a fractal? Instead of giving you a definition of what a fractal is we will
go over the construction of the best known fractals. We start with the simplest
one, the so called Cantor set. This fractal is obtained by taking a segment of
length one and removing the middle third of the set. We don’t remove the ends of
the subinterval, just the numbers in between. We repeat this process with every
segment we obtain, always removing the central third. If we think of numbers as
points in a straight line, then we had the set

and it transformed into

and eventually into

As we did with the Appolonius basket, repeat this process with each of the
segments you find and what is left once we repeat it until no segment is left is a
Cantor set. As before, the set does not contain anything with dimension one (no
segment). But it is formed by a lot of points. In fact, in this case one can even
describe what these points are.

Assume we can make sense of an infinite sum of fractions (and the mentor will
explain to you how you can do that). Assume this fractions will all have powers
of 3 in the denominator, one fraction per power. Assume that the denominators
are all either 0, 1 or 2. These infinite sums are called the triadic expansions of a
number. For example

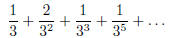
is a triadic expansion. The last tough task in this project is to try to explain why

every point in the cantor set is a number between 0 and 1 having a triadic
expansion with numerators always equal to 0 or 2. Furthermore, every point with
such a triadic expansion is in the Cantor set!

4. Make some drawings

Some fractals are really beautiful. Try to make some drawings of the fractals
we call snowflakes. Take a triangle and draw a equilateral triangle on each side,
with the base in the mid third of the side. Repeat as above to create a fractal. Try
different constructions, be creative and enjoy!