Exponential and Power Functions

Definition 0.1.1 (Power Function). A power function is a function of the form 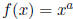, where
a ∈ R.

Thus, a power function is a function where the base of the exponential varies as an input. Very
basic examples of power functions include f(x) = x and f(x) = x². Note that f(x) = x maps
the real numbers to the real numbers, where f(x) = x² maps the real numbers to the nonnegative
real numbers. Some power functions are only defined as maps on the real numbers for a domain of
nonnegative real numbers, such as



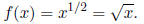
For this function a negative input is not defined, because complex numbers are required to make
sense of the square root of a negative number.

Using power functions as our most basic building blocks, we arrive at polynomial functions.
One of the most basic ways in which we combine functions is in a linear combination.

Definition 0.1.2 (Linear Combination). A linear combination of the functions 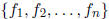is
a function



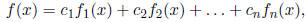
where .

Definition 0.1.3 (Polynomial). A polynomial is a function that can be written as a linear combination
of power functions. Thus, polynomials take on the form



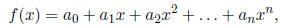
where .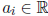

Polynomials provide us with a large class of simple functions to work with. In constrast to
an arbitrary function, a polynomial is very well-behaved, and as a result has a number of useful
properties. As we delve further into the study of calculus we will use polynomials to approximate
other functions, and eventually be able to represent much more complicated functions as infinite
sums of power functions. Such representations are called power series.

In contrast to power functions, exponential functions are functions where the exponent varies
as an input.

Definition 0.1.4 (Exponential Function). An exponential function is a function

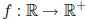(positive real numbers), .

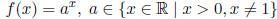Note that when we are talking about exponential functions we are only interested in exponentials
with base a > 0. We are not interested in a = 1, because it is simply a constant function. Since
this constant function behaves differently from the rest of the exponential functions we will deal
with, we simply exclude it from the list of exponential functions. All of the exponential functions
have a domain of R and a range of 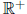(positive real numbers). This means that the output of
an exponential function is always positive. In fact, exponential functions are strictly increasing,
which means for each exponential there is a corresponding inverse function (see theorem ??). These
inverse functions are called logarithms.

Definition 0.1.5 (Logarithmic Function). A logarithmic function is a function



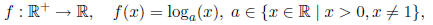
where 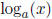is the inverse function of a^x.

Since exponentials and logarithms are inverses, we have



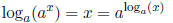
for all a > 0, a ≠ 1. By virtue of this inverse relationship, logarithms inherit a number of useful
properties from exponentials. For instance, by using the relationship



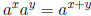
we can deduce



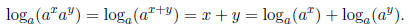
Above we simply use the property that 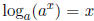, in order to move from step 2 to 3, and step
3 to 4.

We can also deduce a rule for the logarithm of a product, noting that the exponential function
a^x has a range of the entire positive real numbers . In other words, for any 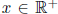there is
some b ∈ R so that



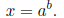
Similarly, for any positive y, we can write y = a^c, for some c. As a result,



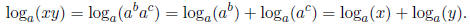
Thus, the logarithm of a product of two numbers is the sum of the logarithms. The full table of
properties of logarithms follows.

Theorem 0.1.2 (Rules of Logarithms). Let 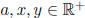. It follows that:



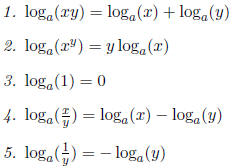
Property 2 above follows if we write , where m ∈ R. Using the inverse relationship
of exponentials and logarithms we also know x = a^m. Thus,



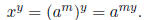
Taking the base a logarithm of each side of the above equation,



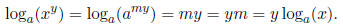
The third property is simply that a⁰ = 1 for all a. Properties 4 and 5 are written only for
convenience - they follow immediately from the previous three properties. Can you see why?

Given that for any value of a > 0, a ≠ 1 we have both an exponential and corresponding
logarithmic function, we have access to a plethora of functions through exponentials and logarithms.
However, as we noted previously, we are currently unable to evaluate exponentials for all but a very
small set of numbers. Similarly, we have difficulty in actually finding the values of logarithmic
functions. Thus, even though we have defined this large class of functions, and have found that
they have a number of useful properties, we still cannot actually evaluate them in most situations.

It turns out that the solution to this problem lies in polynomial functions. Given the difficulty
of evaluating exponential functions, we can instead turn to approximating their values. Using the
power of calculus (through the limit) we will actually be able to represent exponential functions
as a sum of an infinite number of power functions (with natural-number exponents). Since it is
relatively easy to evaluate power functions, this will give us a means of accessing these much more
elusive exponential functions. We will deal with logarithmic functions in a slightly different way,
but calculus will once again be essential.

Although exponential and logarithmic functions define infinite classes of functions, we are really
only interested in a single function from each of these classes. The exponential function we will be
interested in is the base e exponential, where e is a specific irrational number, defined by the limit



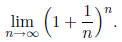
Because this function is used so much more often than other exponential functions, it is often
referred to as the exponential function. Do not worry about understanding the above notation -
as we delve into the study of limits and sequences it will begin to make sense. Corresponding to
the base e exponential, we are interested i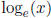n , the natural logarithm, which is often written
as ln(x). The graphs of these two functions are given in figure 1.

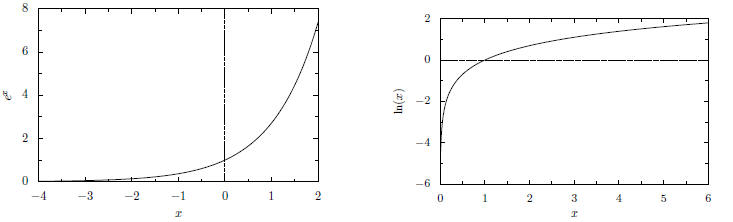
Figure 1: Exponential and Logarithmic Functions

While the exponential function and natural logarithm are really the only two functions of
interest for us, the base 10 logarithm is sometimes encountered as well. The base 10 logarithm
often written log(x) for short, which was widely used to simplify calculations before the advent of
computers. The base 10 logarithmic is a part of the definition of a decibel, so it is encountered in
fields such as telecommunications and acoustics.