Cartesian Coordinate System and Functions

8.2. Function

In the world of Mathematics one of the most common creatures encountered
is the function. It is important to understand the idea of a
function if you want to gain a thorough understanding of Algebra and
Calculus.

Science concerns itself with the discovery of physical or scientific truth.
In a portion of these investigations, researchers (or engineers) attempt
to discern relationships between physical quantities of interest. There
are many ways of interpreting the meaning of the word “relationships,”
but in these lessons we are most often concerned with functional
relationships. Roughly speaking, a functional relationship between
two variables is a relationship such that one of the two variables
has the property that knowledge of it (or knowledge of its value) implies
a knowledge of the value of the other variable.

For example, the physical quantity of area, A, of a circle is related
to the radius of that circle, r. Indeed, it is internationally known
that A = πr²—an equation, I’m sure, you have had more than one
occasion to examine in the past. The simple equation A = πr² sets
forth the principle of a functional relationship: Given knowledge of the
value of one variable (the independent variable), r, then we have total
knowledge of the value of the other variable (the dependent variable),
A. This causal (or deterministic) relationship one variable has with
another variable is the essence of a functional relationship.

This only difference between the example of the previous paragraph
and any other example of a function, either one taken from the applied
fields or one that is of a more “purelyabstract” nature, is the way in
which the functional relationship is defined, and the complexity of that
definition. There are many, many ways of defining (or describing) a
functional relationship between one variable (or a set of variables) and
another variable (or another set of variables). Some of these methods
are rather “natural,” which you will encounter as you continue with
these lessons; others are “unnatural,” but we will not encounter them
at this level of play.

Before we continue with this discussion, perhaps it is best to have a
formalized definition of a function—in the next section.

• The Definition
Definition. Let A be a set and B be a set. A function, f, from A into
B is a rule that associates with each element in the set A a unique
corresponding element in the set B. In this case, we write symbolically,

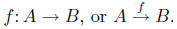
Definition Notes: The set A is called the domain of the function f.
Typically in Algebra and Calculus, the set A will be an interval of the
real number line R. As a notation, we shall refer to the domain of the
function f by Dom( f).

■ The set B is called the codomain of f. The set B may not be
the range of the function.

■  Let the elements of A are referred to by the letter x, and those of
the set B by y. The symbol x is called the independent variable of
f, and y is called the dependent variable. The independent variable
can take on any value in the domain, Dom(f), of f.

■ A function f is a rule that associates with each element, x, in
the set A, a unique corresponding element, y, in the set B. The usual
way we define a function is byan equation that states the relationship
between the variable x and the variable y.

■ For example, let the function f associate the number x with the
number y, where y = x². We write,
f: x → y where y = x²

or, more simply
f: x → x²

thus,
f: 2 → 4
f:−3 → 9
f: 0 → 0

Where, f: 2 → 4 states that f associates with x = 2 the unique
corresponding number y = 4.

■ The above notation is used frequently at higher levels of mathematics,
at our level, we use the standard functional notation. Rather
than writing f: x → x², we simply write f(x) = x².
f(x) = x² means f: x → x2.

Particular evaluations are carried out as follows:
f(2) = 2² = 4
f(−3) = (−3)² = 9
f(0) = 0² = 0

More examples are given below.
■ Given a particular x in Dom(f), y = f(x) is called a value of
the function f. For the function f(x) = x², since f(2) = 4, we can
saythat 4 (y = 4) is a value of f. It should be clear to you that −4
in not a value of the function f(x) = x².

■ For any given function, f, some numbers are values of f while
others are not. The set of all values of a given function is called its
range, denoted by Rng (f); thus,
Rng(f) = { y | y is a value of f }

To be a value, a ‘y’ must be of the form f(x) for some x. Thus,
Rng(f) = { y | y = f(x) for some x in Dom(f) }

■ For the function f(x) = x², the range is
Rng(f) = [0,+∞)

Do you understand why?
All the functions that we encounter in Algebra (and most of those
encountered in Calculus) defined using algebraic expression in one
unknown. For example, the expression x² − 4x + 1 is an algebraic
expression in x. We can use this expression to define a function by
f(x) = x² − 4x + 1

Here are a few examples of functions defined this way. This method is
by no means the only way of defining functions. Read these examples
completely and carefully.

Illustration 1. Examples of functions and numerical evaluations.
(a) Define f by f(x) = x² + x. Then,
f(3) = 3² +3 = 12
f(−3) = (−3)² + (−3) = 6.
(b) Define g by 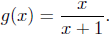Then,


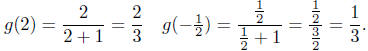
The names of functions are determined by the user, that’s you
and me. I choose a name of g this time.
(c) Define h by 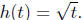Then,

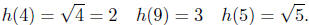
Now I have changed the letter used to denote the independent
variable. I have used t instead of the traditional x—this causes
no problems I hope? Anyletter (or symbol) can be used for the
independent variable, and anyletter (or symbol) can be used
for the dependent variable.

(d) Any symbol you say? How about defining a function W by
W(ø) = ø³. Then,
W(−5) = −125
W(3) = 27

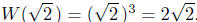
Here, I have used the Greek letter ø (“phi”) for the name of the
independent variable.

Evaluation Tip. To evaluate a function, such as f(x) = x² − 2x, at
a particular value of x = −1, first replace the independent variable
x with the number −1, then evaluate the expression. Thus, f(−1) =
(−1)² − 2(−1) (replace x by −1), then evaluate f(−1) = 1+2 = 3.
Note the use of the parentheses: this is necessary because we are
replacing a single letter x by a compound symbol −1. Not to include
these parentheses (1) is mathematically and notationally wrong, and
(2) invites evaluation errors.

Exercise 8.10. Evaluate each of the functions defined below at the
indicated values. Passing is 100%.
(a) f(x) = 2x² − 3x; f(2), f(−2), f(−1/2)
(b) g(s) = s(s + 1)(s + 2); g(0), g(1), g(−1), g(−3)
(c) 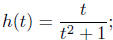  h(1), h(−2), h(1/2), h(−1/2)
(d) D(w) = 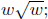  D(9); D(1/9)

• For those Who want Greater Insight. Models for Functions.
Listed behind this link is a description of several ways in which we
can view a function. These points of view mayhelp you to understand
this important mathematical object.

• The Domain of a Function
In the examples in the previous paragraphs, nothing was mentioned
concerning the domains of the functions considered. In this section
we briefly discuss methods of computing the domain of a function.
The domain of the function defined is either (1) explicitly specified or
is (2) not explicitly specified. (That seems reasonable.)

Illustration 2. Examples of functions with explicitly specified domains.
(a) Define a function f by
f(x) = x², x≥ 1

Here, we are explicitlydefining the domain of f to be
Dom(f) = [1,+∞) = { x | x ≥ 1 }

For this function, f(2) = 4 is defined, but f(0) is not because
x = 0 does not fall into the specified domain.

(b) Define a function g by
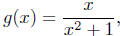  0 ≤ x < 1
Here, we have specified the domain of g to be
Dom(g) = [0, 1 ) = { x | 0 ≤ x < 1 }

Illustration Notes: Such (artificial) restriction of the domains may
arise from physical considerations. Perhaps these functions, f and g
above, are modeling some physical system; within the context of this
physical system, it only make sense to consider x ≥ 1, in the case of
the function f, and 0 ≤ x < 1 in the case of g.

When the domain of a function at definition time is left unspecified,
that usually means we are to take as the domain the so-called natural
domain of the function.

The Natural Domain of a function. Given a function y = f(x). The
natural domain of f is the set of all real numbers, x, for which the
value f(x) can be calculated as a real number.

The next example illustrates the reasoning and methods used to calculate
the natural domain of a function. Read carefully!

Example 8.2. Compute the natural domain of each of the following.
(a) f(x) = x² + 3x + 1

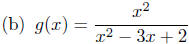
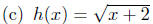
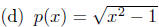
Strategy. Let y = f(x) be a function, where f(x) is some algebraic
expression. The natural domain consists of all x for which . . .
• the denominator (if any) is not equal to zero; and
• anyradicands of even roots (if any) are nonnegative.
Here’s another example that incorporates all components of the above
strategy.

Example 8.3. Find the natural domain of

Quite typically, the strategy involves setting up some constraints or
conditions on the values of the independent variable in the form of
inequalities. Once you identify these inequalities, you solve them (possibly using
the Sign Chart Method). The natural domain is then the
set of all values of the independent variable that satisfy all the constraints
or conditions.

Exercise 8.11. Compute the natural domain of each of the following.

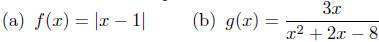
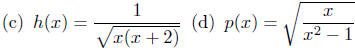
• Points of Intersection of Curves
We have seen in the previous section that determining the natural
domain of a functions oftimes require the setting up and solving of
inequalities. To determine where two curves intersect, if at all, we must
be able to set up and solve equations. This is why the basic mechanics
of solving inequalites and equations are so important—equations
and inequalities are the natural way n which we ask questions and
the techniques of solutions are the way we are able to answer these
questions.

Determining the x-intercept. Let y = f(x) be a function. The xintercept,
if there is one, is that value of x such that f(x) = 0. As
you know, every function has a graph—graphing will be taken up in
Lesson 9—and in terms of the graph the x-intercept is the location
on the x-axis where the graph crosses the x-axis.

Procedure. To find the x-intercept(s) of the function y = f(x), set up
the equation
f(x) = 0 (5)
and solve for x.

Exercise 8.12. Find the x-intercept(s), if any, of each of the following
functions.
(a) f(x) = 4x − 1
(b) f(x) = x² − 3x + 2
(c) f(x) = x³ + 6x² ++8x
(d) f(x) = x² + x + 1
(e) f(x) = 2x² − x −1
f)f(x) = x² + x − 3

Exercise 8.13. What does the problem of finding the x-intercept of
a function have to do with the title, “Points of Intersection of Curves,”
of this section?

Determining the intersection of two Curves. Consider the two functions
y = f(x) and y = g(x). We wish to find all points, if any, on the
intersection of the graphs of f and g.

Let (x₀, y₀) be a point that is on both graphs of f and g. This means
f(x₀) = y₀ and g(x₀) = y₀.

At this point, we have f(x₀) = y₀ = g(x₀). This represents a criterion
for finding the points of interection of two graphs.

Procedure. Let y = f(x) and y = g(x) be two function. Set up the
equation
f(x) = g(x) (6)

and solve for x.
Finding the points of intersection is essentially a problem in solving
equations.

Example 8.4. Find the points of interection beween
(a) f(x) = 3x + 2 and g(x) = 5x − 4
(b) f(x) = x² − 3x + 1 and g(x) = 2x − 5

Notice that the points of intersection can be calculated without reference
to the graph of the functions. At our level of play, finding the
points of intersection is purely an exercise in algebra.

Exercise 8.14. Find the cartesian coordinates of the points of intersections
of each of the following pairs of functions.
(a) f(x) = 6x + 3 and g(x) = 2x − 7
(b) f(x) = x + 3 and g(x) = 2 − 8x
(c) f(x) = x² + 7x − 1 and g(x) = 4x − 3

Now for some exercises that require the use of the Quadratic Formula.

Exercise 8.15. Find the abscissas of intersection of each of the following
pairs of functions.
(a) f(x) = 2x² − 5x + 2 and g(x) = x + 3
(b) f(x) = x² + 4x − 1 and g(x) = 1 − 4x − x²
(c) f(x) = 3x² + 1 and g(x) = x² − 5x
Some curves do not intersect. Investigate these kind.

Exercise 8.16. Verify algebraically that each pair of functions do
not intersect.
(a) f(x) = 4x − 2 and g(x) = 4x + 12
(b) f(x) = 2x² + 3 and g(x) = x² − 1
(c) f(x) = x² + 2x + 2 and g(x) = x + 1
(d) f(x) = x² − 2x − 4 and g(x) = 4x² − 3

 

We have come to the end of Lesson 8. Congratulations of reaching
this far. In Lesson 9, we take up the topics of linear and quadratic
functions as well as some graphing topics.