Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Linear Equations and Linear Functions

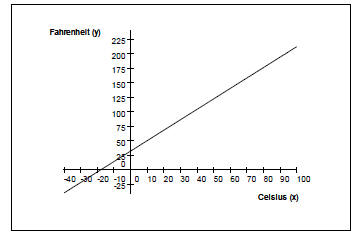
It will be shown in the next section that when x is the temperature in
Celsius degrees and y is the temperature in Fahrenheit degrees,
the numbers x and y satisfy the equation 9x-5y =-160.
From the graph below, it appears that a straight-line relationship
exists between these two quantities.
In fact, 9x-5y =-160 is called a linear equation in two variables.

Definition: Any equation that can be put in the form Ax+By = C,
where A, B, and C are real numbers and A and B are not both 0,
is called a linear equation in two variables. The graph of any equation
of this form is a straight line (that is why these equations are called ”linear”).
The form Ax+By = C is called the standard form of a linear equation in
two variables.

An ordered pair (x, y) whose coordinates satisfy an equation in two variables
is called a solution of the equation. The graph of an equation in two variables
is formed by graphing the set of all solutions to the equation.

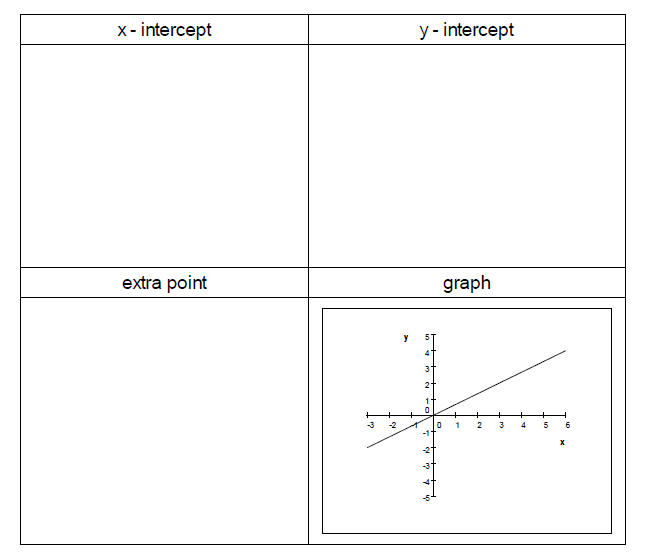
Example 1 Find the intercepts of 3x-4y = 18. Sketch the graph.

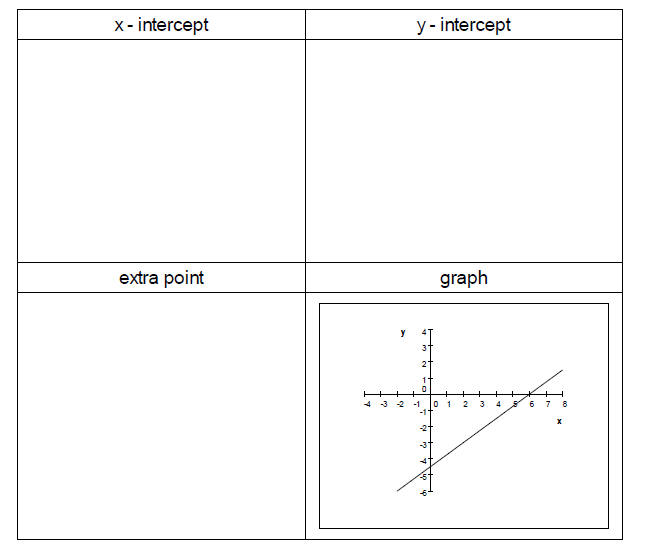
Example 2 Find the intercepts of the equation 2x-3y = 0. Sketch the graph.

Graphing Horizontal and Vertical Lines
Example 3 Find the intercepts of the line y = 3. Sketch the graph.

Equations of horizontal lines have the form y = k,
where k is the y-coordinate of every point on the line.

Example 4 Find the intercepts of the line x = 2. Sketch the graph.

Equations of vertical lines have the form x = k,
where k is the x-coordinate of every point on the line.

All linear equations except for equations of the form x = k are functions.
All linear equations of the form Ax+By = C are functions if B≠0.

Example 5 Assume that B≠0 and solve the linear equation Ax+By = C for y.

A linear function is a function that can be written in the form

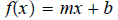
where m and b a real numbers. The graph of a linear function is a nonvertical line.

Example 6 Compare each of the following functions to 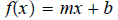and indicate
which ones are linear.

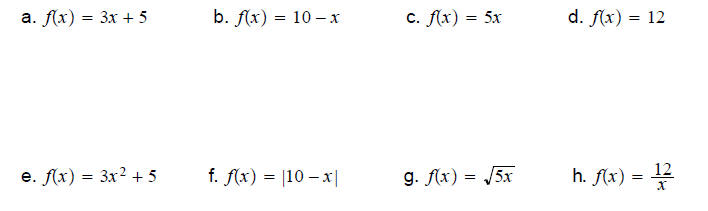
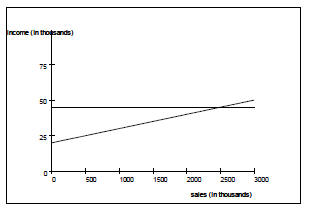
Example 7 Tanya works for Prentice Hall as a textbook representative.
The linear function
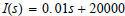
describes her annual income I when she has total sales s.

(a) What is the implied domain of this linear
function?

(b) What is I(0)? What does this mean?

d) Graph the function

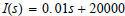
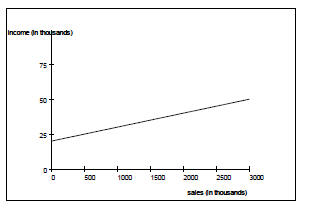
(e) At what level of sales will Tanya’s income be
$45,000?

A+ Algebra Resources

We will end your math anxiety

Linear Equations and Linear Functions

More Tutorials