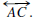A Quick Review of Elementary Euclidean Geometry
0.1 MEASUREMENT AND CONGRUENCE
0.2 PASCH’S AXIOM AND THE CROSSBAR THEOREM
0.3 LINEAR PAIRS AND VERTICAL PAIRS
0.4 TRIANGLE CONGRUENCE CONDITIONS
0.5 THE EXTERIOR ANGLE THEOREM
0.6 PERPENDICULAR LINES AND PARALLEL LINES
0.7 THE PYTHAGOREAN THEOREM
0.8 SIMILAR TRIANGLES
0.9 QUADRILATERALS
0.10 CIRCLES AND INSCRIBED ANGLES
0.11 AREA
This preliminary chapter lays out the basic results from
elementary Euclidean
geometry that will be assumed in the course. Those readers who are using this
book
as a supplement to a course in the foundations of geometry should omit the
chapter
and simply refer to it as needed for a summary of the notation and terminology
that
will be used in the remainder of the book. Readers who are using this book as a
stand-alone text in Euclidean geometry should study the chapter carefully
because
the material in this chapter will be used in later chapters.
The theorems stated in this chapter are to be assumed
without proof; they
may be viewed as an extended set of axioms for the subject of advanced Euclidean
geometry. The results in the exercises in the chapter should be proved using the
theorems stated in the chapter. All the exercises in the chapter are results
that will
be needed later in the course.
We will usually refer directly to Euclid’s Elements when
we need a result
from elementary Euclidean geometry. Several current editions of the Elements are
listed in the bibliography (see [4], [5], or [10]). The Elements are in the
public
domain and are freely available on the world wide web. Euclid’s propositions are
referenced by book number followed by the proposition number within that book.
Thus, for example, Proposition III.36 refers to the 36th proposition in Book III
of
the Elements.
0.1 MEASUREMENT AND CONGRUENCE
For each pair of points A and B in the plane there is a nonnegative number AB,
called the distance from A to B. The segment from A to B, denoted
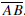 consists of A
consists of A
and B together with all the points between A and B. The length of
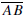 is the distance
is the distance
from A to B. Two segments 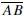 and
and
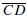 are congruent, written AB >
are congruent, written AB >
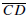 , if they
, if they
have the same length. There is also a ray 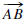 and
a line
and
a line 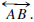
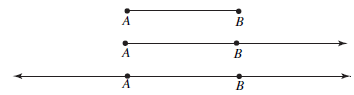
FIGURE 0.1: A segment, a ray, and a line
For each triple of points A, B, and C with A ≠ B and A ≠ C
there is an angle,
denoted 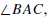 that is defined by
that is defined by
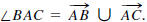 The measure of the angle
The measure of the angle
is a number 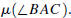 We will always measure angles in
degrees and assume that
We will always measure angles in
degrees and assume that
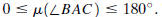 The measure is 0° if
the two rays
The measure is 0° if
the two rays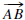 and
and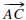 are equal; the
are equal; the
measure is 180° if the rays are opposite; otherwise it is
between 0° and 180° . An
angle is acute if its measure is less than 90° , it is
right if its measure equals 90° , and
it is obtuse if its measure is greater than 90° . Two
angles are congruent if they have
the same measure.
The triangle with vertices A, B, and C consists of the
points on the three
segments determined by the three vertices; i.e.,
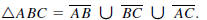
The segments  are
called the sides of the triangle ΔABC. Two
are
called the sides of the triangle ΔABC. Two
triangles are congruent if there is a correspondence between the vertices of the
first
triangle and the vertices of the second triangle such that corresponding angles
are
congruent and corresponding sides are congruent.
Notation. It is understood that the notation ΔABC
 ΔDEF means that the two
ΔDEF means that the two
triangles are congruent under the correspondence
A ↔ D, B ↔ E, and C ↔ F. The
assertion that two triangles are congruent is really the assertion that there
are six
congruences, three angle congruences and three segment congruences.
Specifically,
ΔABC  ΔDEF means
ΔDEF means
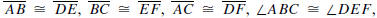
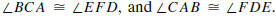 In high school this is often
abbreviated
In high school this is often
abbreviated
CPCTC (corresponding parts of congruent triangles are congruent).
0.2 PASCH’S AXIOM AND THE CROSSBAR THEOREM
The two results stated in this section specify how one-dimensional lines
separate
the two-dimensional plane. Neither of these results is stated explicitly in
Euclid’s
Elements. They are the kind of foundational results that Euclid took for
granted.
The first statement is named for Moritz Pasch (1843–1930).
Pasch’s Axiom. Let ΔABC be a triangle and let
ℓ be
a line such that none of the
vertices A, B, and C lie on ℓ.If
 intersects
intersects
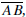 then ℓ also intersects either
then ℓ also intersects either
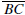 or
or 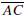
(but not both).
Let A, B, and C be three noncollinear points. A point P is
in the interior of
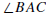 if P is on the same side of
if P is on the same side of
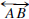 as C and on the same side of
as C and on the same side of
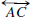 as B.
as B.
Note that the interior of
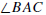 is defined provided
is defined provided
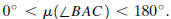
It would be reasonable to define the interior of
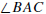 to be the empty set in case
to be the empty set in case
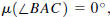 but there is no interior for an angle of
measure 180 . The segment
but there is no interior for an angle of
measure 180 . The segment
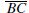 is called a crossbar for
is called a crossbar for
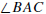
Crossbar Theorem. If D is in the interior of
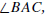 then there is a point G such that
then there is a point G such that
G lies on both 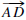 and
and
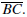
0.3 LINEAR PAIRS AND VERTICAL PAIRS
Angles 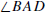 and
and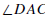 form a linear pair if A, B, and C are collinear and A is
form a linear pair if A, B, and C are collinear and A is
between B and C.
Linear Pair Theorem. If angles
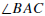 and
and 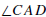 form a linear pair, then
form a linear pair, then
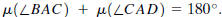
Two angles whose measures add to 180°
are called supplementary angles or
supplements. The Linear Pari Theorem asserts that if two angles form a linear
pair,
then they are supplements.
Angles 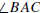 and
and
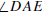 form a vertical pair (or are vertical
angles) if rays
form a vertical pair (or are vertical
angles) if rays 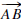
and 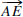 are opposite and rays
are opposite and rays
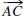 and are opposite or if rays
and are opposite or if rays
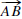 and
and 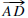 are
are
opposite and rays 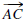 and
and
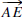 are opposite.
are opposite.
Vertical Angles Theorem. Vertical angles are
congruent.
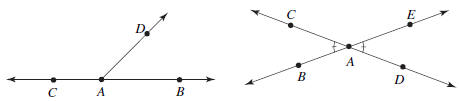
FIGURE 0.2: A linear pair and a vertical pair
The linear pair theorem is not found in the Elements
because Euclid did
not use angle measure; instead he simply called two angles ‘‘equal’’ if, in our
terminology, they have the same measure. The vertical angles theorem is Euclid’s
Proposition I.15.
0.4 TRIANGLE CONGRUENCE CONDITIONS
If you have two triangles and you know that three of the parts of one are
congruent
to the corresponding parts of the other, then you can usually conclude that the
other
three parts are congruent as well. That is the content of the triangle
congruence
conditions.
Side-Angle-Side Theorem (SAS). If ΔABC and ΔDEF are
two triangles such that
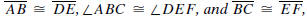 then ΔABC
then ΔABC 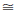 ΔDEF.
ΔDEF.
Euclid used his ‘‘method of superposition’’ to prove SAS
(Proposition I.4),
but it is usually taken to be a postulate in modern treatments of geometry. The
next
two results (ASA and AAS) are both contained in Euclid’s Proposition I.26 and
the
third (SSS) is Euclid’s Proposition I.8.
Angle-Side-Angle Theorem (ASA). If ΔABC and ΔDEF
are two triangles such
that 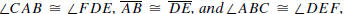 then ΔABC
then ΔABC
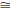 ΔDEF.
ΔDEF.
Angle-Angle-Side Theorem (AAS). If ΔABC and ΔDEF
are two triangles such
that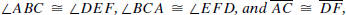 then ΔABC
then ΔABC
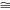 ΔDEF.
ΔDEF.
Side-Side-Side Theorem (SSS). If ΔABC and ΔDEF are
two triangles such that
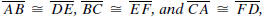 then ΔABC
then ΔABC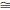 ΔDEF.
ΔDEF.
There is no Angle-Side-Side condition, except in the
special case in which the
angle is a right angle.
Hypotenuse-Leg Theorem (HL). If ΔABC and ΔDEF are
two right triangles with
right angles at the vertices C and F, respectively,
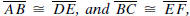 then
then
ΔABC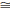 ΔDEF.
ΔDEF.
EXERCISES
0.4.1. Use SAS to prove the following theorem (Euclid’s Proposition I.5).
Isosceles Triangle Theorem. If ΔABC is a triangle and
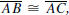 then
then 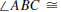
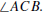
0.4.2. Draw an example of two triangles that satisfy the ASS condition
but are not
congruent.
0.4.3. The perpendicular bisector of a segment
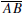 is a line ℓ such that ℓ intersects
is a line ℓ such that ℓ intersects
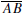 at
at
its midpoint and 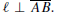 Prove the following
theorem.
Prove the following
theorem.
Pointwise Characterization of Perpendicular Bisector. A point P lies on
the
perpendicular bisector of 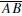 if and only if PA
= PB.
if and only if PA
= PB.
0.4.4. The angle bisector of 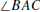 is a ray
is a ray
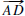 such that
such that 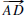 is between
is between 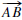 and
and
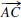 and
and
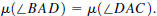 The distance from a point to a line is
measured along a
The distance from a point to a line is
measured along a
perpendicular. Prove the following theorem.
Pointwise Characterization of Angle Bisector. A point P lies on the
bisector of
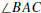 if and only if P is in the interior of
if and only if P is in the interior of
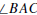 and the distance from P to
and the distance from P to
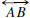
equals the distance from P to