Calculus I - Related Rates
Related Rates Problems
Another common application of the derivative involved
situations in which two or more related quantities are changing
with time.
These are called related rates problems.
Example
Suppose the radius of a circle is increasing at 7 cm/s. How fast
is the area increasing when the radius is 20 cm?
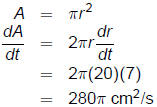
Guidelines
1 If possible, draw a picture to illustrate the problem
and
label the pertinent quantities.
2 Set up an equation relating all of the relevant quantities.
3 Differentiate (implicitly) both sides of the equation
with
respect to time (t).
4 Substitute in the values for all known quantities and rates.
5 Solve for the remaining unknown rate.
Example
A painter is painting a house using a ladder 15 feet long. A dog
runs by the ladder dragging a leash that catches the bottom of
the ladder and drags it directly away from the house at a rate of
22 feet per second. How fast is the top of the ladder moving
down the wall when the top of the ladder is 5 feet from the
ground?
Example
For the previous situation, how fast is the angle between the
ground and the ladder changing when the top of the ladder is 5
feet from the ground?
Example
Two ships sail from the same port. The first ship leaves port at
1:00AM and travels east at a speed of 15 nautical miles per
hour. The second ship leaves port at 2:00AM and travels north
at a speed of 10 nautical miles per hour. Determine the rate at
which the ships are separating at 3:00AM.
Example
A revolving beacon in a lighthouse located 3 miles from a
straight shoreline makes 2 revolutions per minute. Find the
speed of the spot of light along the shore when the spot is 2
miles from the point on the shore nearest the lighthouse.
Example
Flour sifted onto waxed paper forms a pile in the shape of a
cone with equal radius and height. The volume of flour in the
pile is increasing at a rate of 7.26 in3/s. How fast is the height of
the flour increasing when the volume is 29 in3?
Homework
Read Section 3.8
Pages 324-327: 1–39 odd

