Math Practice Midterm 1

Part I: No calculators allowed.

1. Write each expression without negative exponents, and simplify.

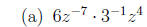
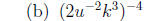
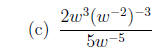
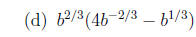
2. Solve each equation.

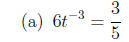
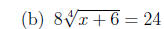
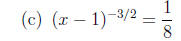
3. Solve each quadratic equation, either by factoring or by completing the square. You
will receive no credit for using the quadratic formula to obtain an answer. (Hint: the
discriminant can help you decide what method to use.)

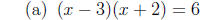
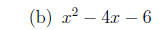
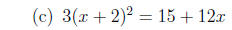
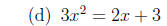
4. Solve each quadratic inequality.

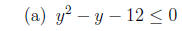
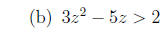
5. Solve algebraically:

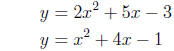
6. The intensity of illumination from a light source varies inversely with the square of the
distance from the source. If a lamp has an intensity of 100 lumens at a distance of 3
feet, what is its intensity 8 feet away?

7. A small company manufactures radios. When it charges $20 for a radio, it sells 500
radios per month. For each dollar the price is increased, 10 fewer radios are sold per
month.

(a) Write an equation for the monthly revenue in terms of x, where x represents the
price increase over the base price of $20.

(b) What should the company charge for a radio in order to maximize its monthly
revenue?

8. For each of the following quadratic functions, nd the coordinates of the vertex and
the intercepts (x and y).

(a) f(x) = x² + x - 6

(b) y = 8 - x - 2x²

9. The period, T, of a pendulum varies directly with the square root of its length, L.

(a) Express T as a function of L. Let k stand for the constant of variation.

(b) Make a rough sketch of the graph of your function (you don't know k, so focus on
the qualitative features).

(c) If a certain pendulum is replaced by a new one that is four- fifths as long as the old
one, what happens to the period?

Part II: You will need to use a calculator on this part.

10. For each of the following tables, y varies either directly or inversely with a power of
x. Find the power of x and the constant of variation, k. Write a formula of the form

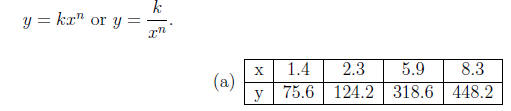
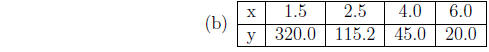
11. Suppose the rate of growth of a population, R, is proportional to a power of the current
population, P, so that its formula is given by

R = 0:015P^1.2,

where P is measured in thousands and R is measured in thousands per year.
(a) Find R when P = 20, when P = 40, and when P = 60.

(b) What will the population be when its rate of growth is 5000 per year? (Be careful
with your units!)

12. Solve the inequality -6x² - 36x - 20 ≤ 25.36.