Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Math 125 Exponents

Exponents are numbers that indicate a repeated factor. It tells you to a multiply a
number times itself a certain number of times. For example:

4³ = x	4³ is read as 4 to the third power. Usually a number to the third power is said to be cubed. So you would read this as four cubed. Four is the factor and three is the exponent. The exponent tells you how many times to multiply the factor by itself.
4 4 4 is the same as 4³	Now simplify. Remember to do multiplication from left to right.
16 * 4 64 = x	4³ is 64.

How to read exponents:

4² is read as four squared.
4³ is read as four cubed.
4⁴ is read as four to the fourth.
4⁵ is read as four to the fifth.
. . .

Hints:

~ A number (x) to the power zero (0) is one (1). 5⁰ = 1
~ A number (x) to the power one (1) is the number (x). 5¹ = 5

Addition/Subtraction:
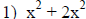	When adding/subtracting numbers with exponents, just add/subtract the coefficients. Note: The powers on the variables MUST be the SAME.
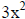	Solution: 3x²
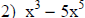	The exponents are not the same. One is cubed and the other is to the fifth power. So they cannot be added together.
	Solution: x³ + 5x⁵
Multiplication:
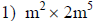	When multiplying numbers with exponents, just multiply the coefficients. Then, carry over the variable and add the exponents.
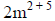	When you multiply the coefficients, you get 2. Then you carry over the m. Next, add the exponents of the variable together.
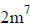	2 + 5 is 7
	Solution: 2m⁷
Division:
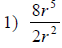	When dividing monomials (single terms), just divide the coefficients.
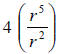	In division, subtract the powers of like variables. If the larger exponent is on the top, subtract the bottom from the top. If the larger exponent is on the bottom, subtract the top from the bottom. Place the final answer where the larger exponent was (numerator or denominator).
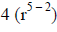	The variable (r) goes in the numerator because the larger exponent (5) was in the numerator. Simplify.
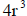	5 - 2 is 3.
	Solution: 4r³
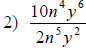	Divide coefficients.
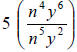	Subtract exponents of like variable. n will be in the denominator because 5 is larger than 4. y will be in the numerator because 6 is larger than 2.
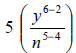	Simplify.
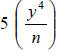	6 - 2 is 4. 5 - 4 is one. Coefficients one are not written. Now multiply times 5.
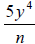	Solution: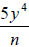
Power to Power:
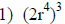	Here, a number with a power is being raised to another power. Raise all coefficients to the outside power. Raise any variable to the outside power by carrying over the variable and multiplying the exponents.
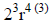	Simplify.
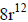	2 cubed is 8. 4 times 3 is 12.
	Solution: 8r¹²

Negative Exponents:

~ If a term in the numerator has a negative exponent, move it to the
denominator. Change the negative sign to a positive.

~ If a term in the denominator has a negative exponent, move it to the
numerator. Change the negative sign to a positive.

Note: If after all negative exponents are moved there are no terms left in either the
numerator or the denominator, then put a 1 there.

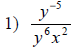	Move the y^-5 to the denominator to make the exponent positive.
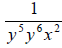	The exponent became positive and there were no terms in the numerator, so one is placed there. Now multiply like terms.
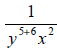	Simplify.
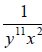	Solution: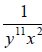

Scientific Notation: Numbers in scientific notation are expressed as

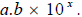
Note:

~ In scientific notation a has to be a whole number greater than or equal to1 and
less than 10, and b can be any number.

~ If the decimal point is not shown, it is to the right side of the ones digit.

~ If the original number is greater that 10, the exponent (x) is positive. If it is
less than 1 it is negative.

Standard Notation to Scientific Notation
1) Express 800 in scientific notation.	To express 800 in scientific notation, you have to get a.
8.00. ←	To get a, you move the decimal point, so that the number becomes an integer between 0 and 10. You have to move the decimal point 2 places to the left to make the number an integer between 0 and 10. The amount of places you move the decimal point is the exponent of the 10, so the scientific notation for 800 is 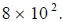Solution:
2) Express .0098 in scientific notation. .009.8 →	To get a, you have to move the decimal point three places to the right, so the number becomes 9.8 (an integer between 0 and 10). Since the decimal was moved three places to the right, the exponent of the ten is –3, so the scientific notation for .0098 is 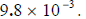Solution:
Scientific Notation to Standard Notation
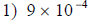
.0009. 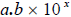←	Using this formula, determine what a is. In this problem a is 9. x tells how many spaces to move the decimal point of a. If x is positive, move the decimal point to the right. If x is negative, move the decimal point to the left. x is –4. So, move the decimal point of a four spaces to the left. Solution: .0009

A+ Algebra Resources

We will end your math anxiety

Math 125 Exponents

More Tutorials