Slope-Intercept and Point-Slope Forms of a Linear
To determine the equation of a line, you may use two
variations of the general form of a line.
These formulas are:
1)The Point-Slope Formula
(y – y1) = m(x – x1)
2)The Slope-Intercept Formula y = mx + b
As the names imply the form that you use is dependant on the information you are given to start with.
Example 1: Find the equation of the line that has a slope of 1/3 and contains the point (2, -1).
Solution
Since the information given is a point and the slope, the point slope formula is
used.
Step 1: Substitute the given into the formula.
Since m = 1/3 and P1 = (2, -1) then x1 = 2 and y1 = -1.
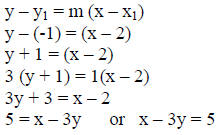
(This the standard formula of the line)
Step 2: Calculate P2.
Select any value you with for x or y and substitute it
into the equation found in
step 1. For this example y will equal 2.
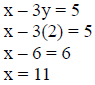
Therefore P2 = (11, 2)
Step 3: Verify.
When any two points of a line are substituted into the
slope formula the slope of
the line should be the answer. In this case, when
P1 and P2 are
substituted into
the slope formula the answer should be 1/3.
SinceP1 = (2, -1) and P2 = (11, 2) then x1 = 2, x2 = 11, y1 = -1 and y2 = 2 then:
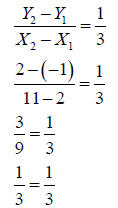
(The slopes are alike so the equation and P2 are correct)
Step 4: Graph
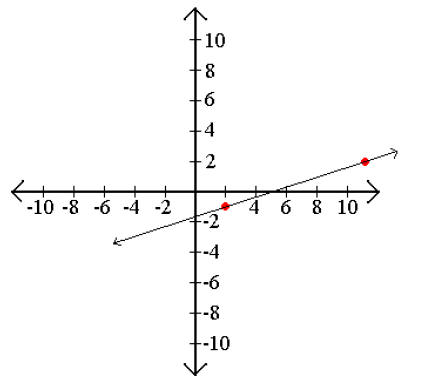
The slope intercept formula y = mx + b is used when you know the slope of the line to be examined and the point given is also the y intercept (0, b). In the formula, b represents the y value of the y intercept point.
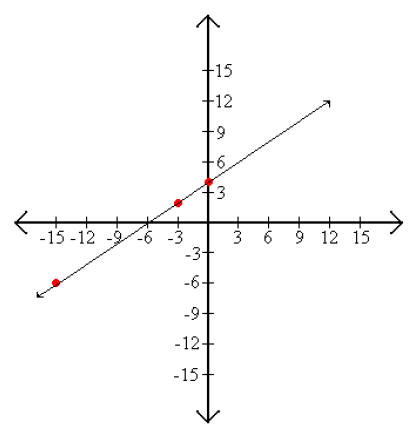
Example 2: Find the equation of the line that has a slope of 2/3 and a y intercept of (0, 4).
Solution
Step 1: Substitute the given into the formula.
Since the y intercept is (0, 4), b = 4 and the slope, m, is given as 2/3.
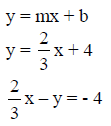
(Note: The standard form does not allow fractional values,
so you need to
resolve this by multiplying by the LCD of 3).
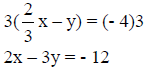
(This is the calculated equation of the line.)
Step 2: Verify.
Plot 2 points using the formula. For this example y1 = 2 and y2 = -6.
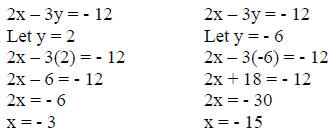
Therefore P1 = (-3, 2) and P2 = (-15, -6)
Step 2:
Next the x and y values are substituted into the slope formula.
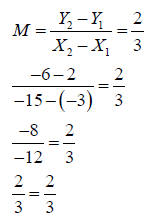
Since the slope found using the two points is also 2/3 the formula is correct
Step 3: Graph