Review of Techniques of Integration
Strategy
• Identify the type of integral you have.
• Try using the simplest technique for your integral.
• If that doesn’t work, try the next-level method
(might involve more work, but is more likely to
work).
• You may have to break-up the integral into several
parts and use a different method for each
part.
u-Substitution
Goal:
Reduce the integral to one of the 10 basic
integrals in the table.
Works:
If the integrand is nice enough to have exactly
the chain rule form: 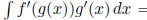
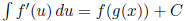
Examples: 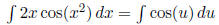
Integration by parts
Goal:
Figure out the integral of a product of two functions
(polynomials, exponentials, logs, trig, inverse
trig, etc).
Works: For all the times when u-substitution fails
Notes:
Needed for  (Use Trig-Tricks for
(Use Trig-Tricks for
most other trig integrals)
Examples: 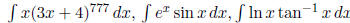
Trig Tricks
Goal: Integrals of combinations of trig functions
Examples: 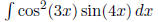
The 4 steps
Check these steps (in order!) to simplify your integral
as much as needed:
1: 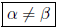 If you have an integral of a product of
If you have an integral of a product of
trig functions with different angles (Ex: 3x ≠
4x) you MUST use trig identities to break it
up into a sum of different terms before you can
make any progress:
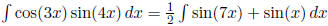
2: If one is odd, u = other This gives the right
u-substitution for 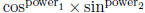 integrals
integrals
(with positive or zero powers). You will also
need to use cos2 x + sin2 x = 1.. Example:
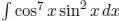 then
then 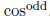 , so
u = sin x and
, so
u = sin x and
use cos2 x = 1 − u2 to get
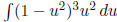
3: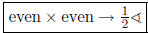 If both powers
are even,
If both powers
are even,
then you need to use the half-angle formulas:
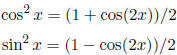
4: SET TOS Use sec2 x = 1 + tan2 x with
• SET: 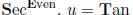
• TOS: 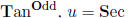
Ex: 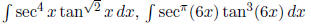
Square roots
• If you have a
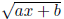 then let u =
then let u =
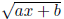 so
so
u2 = ax+b and 2u du = a dx and x = (u2−b)/a
• If you have a
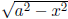 then
then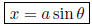
• If you have a
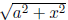 then
then
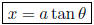
• If you have a
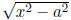 then
then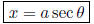
• If you have a
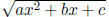 then First,
then First,
complete the square, then let u = x−d and
look again, example:
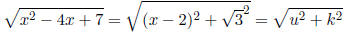
• These work with positive or negative powers of
the roots and (quadratic)±k too.
Rational Functions
| “Rational fcn” means | polynomial |
| polynomial |
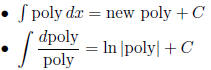
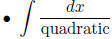 : Complete the square and use
: Complete the square and use
square roots guide.
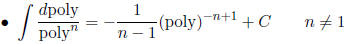
Everything else needs Partial Fractions:
1. NO Improper fractions: Convert 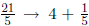 .
.
You MUST do this first! (Use long division or
synthetic division)
2. Factor numerator, denominator, cancel stuff
3. Expand out as a sum of partial fractions (each
will be one of the “easy ones”)

