Math 544 Exam 1 Information
Topic List (not necessarily comprehensive):
You will need to know how to define vocabulary words/phrases defined in class.
1.1: Matrix representation of a linear system: coefficient matrix, augmented
matrix, elementary
row operations, row equivalence.
1.2: Solving linear systems via Gauss-Jordan elimination: echelon and
reduced echelon
forms of a matrix, identifying dependent and independent variables, recognizing
when a
system is consistent/inconsistent.
1.3: Relationship between the number of nonzero rows, the number of leading
1’s, and the
number of columns in an augmented matrix in reduced echelon form.
Homogeneous linear
systems. The number of possible solutions to (for example)
1. a general linear system.
2. an m*n system with m < n.
3. a homogeneous system.
1.5: Matrix operations: addition, multiplication, multiplication by scalars, dot product in Rn.
1.6: Properties of matrix addition, multiplication, and multiplication by
scalars. The matrix
transpose and its properties. What is the transpose of a product? What is a
symmetric matrix?
Also vector norm (length) in terms of the dot product.
1.7: Linear combinations, linear dependence/independence: determinination of
whether
a given set of vectors is linearly dependent/independent. Non-singular matrices
(remember,
only square matrices can be singular or non-singular!); conditions equivalent to
nonsingularity
of
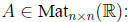
1. Ax = θ has only the trivial solution x = θ
2. columns of A are linearly independent
3.
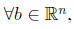Ax = b has a unique solution.
4. A is invertible.
5. A is row equivalent to the identity, In.
1.9: Matrix inverses: existence of inverses (see above, e.g., A is invertible
<-> A is nonsingular),
using inverses to solve systems, computing inverses by row reduction, formula
for
inverse of 2*2 matrix, algebraic properties of inverses (e.g., what is the
inverse of a product
of two matrices?) Remember, only square matrices can be invertible.
Notes:
•Only sets of vectors can be linearly dependent/independent. It does not make
sense to
speak of matrices or systems of equations being linearly dependent/independent.
•Only systems of linear equations can be consistent/inconsistent. It does not
make sense
to speak of matrices or sets of vectors as consistent/inconsistent.
•Only squares matrices can be singular/non-singular. It does not make sense
to speak of
a system of equations or set of vectors as being singular/non-singular. The same
applies for
invertibility.
