Matrix Operations

Theorem. If the columns of C each sum to less than 1, and the entries
in 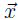are non-negative, then (I  - C) is invertible, and the production vector
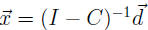has nonnegative entries and is the unique solution to

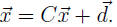
Expanding the problem.
If the external demand is 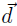, the various sectors can produce 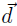units, but this
will create an intermediate demand of .
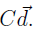They can then produce another 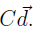units. This leads to further intermediate
demand of 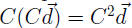units.

They can then produce another 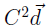units. This leads to further intermediate
demand of 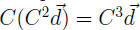units.

Adding up all of the above, in total the industries have to produce this to satisfy
the external final demand as well as all of the internal demands that arise as a
result.

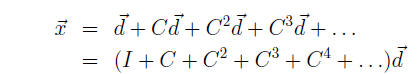
Now for a trick to see this sum in another way. Let
W = I + C + C² + C³ + . . . + C^m

Then

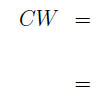
and so
W - CW = (I - C)W =

If the columns of C each sum to values strictly less than 1, the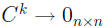n (an
n × n matrix of zeros) as 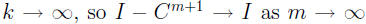. And by the
Theorem, (I  - C) is invertible, and so

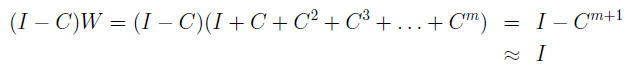
which implies
I + C + C² + . . . + C^m ≈ (I  - C)^-1

if the column sums of C are less than 1. We can make the approximation as
accurate as desired by making m sufficiently large.

In practice, this can be a useful approximation, especially if the matrix is large
and sparse (i.e., contains many zeros) and the column sums are significantly
less than one. Even a standard linear system 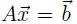can be rewritten to use
this trick, by letting C = I  -A. Then we can write the system as

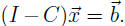
Economic meaning of entries in (I  - C)^-1.

Given external demand 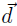, say we have found the solution (production vector)
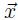satisfying
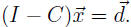
Now consider a new external demand 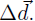Say we have solution
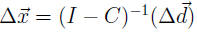satisfying

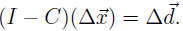
If we let 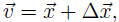then

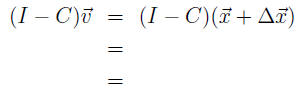
because everything is linear.

Now say 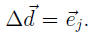Then we have solution 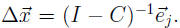  But this is just
the _______________________________of (I  -C)^-1 ! So if we increase external
demand from 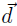up to 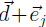, we need to increase production from
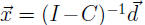
to 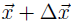, where .

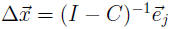Result:The j^th column of (I  - C)^-1 says how much extra production will
be needed from all sectors, to meet one additional unit of demand for sector j.

Because the production vector 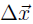contains the production levels for each sector,
and because 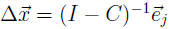, we can go even further, and get.

Result :The number in row i, column j of (I  - C)^-1 says how much extra
production will be required of industry i in order to meet an increase in exter-
nal demand of one unit of sector j, taking into account the new intermediate
demands which arise.

This could also be written as the partial derivative

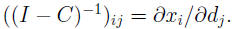
Section 2.8 { Subspaces, Basis for Null Space and Column Space

Note. examples labeled with Arabic numbers are examples from the book, examples labeled with Roman
numerals are not.

Subspaces
Definition Given a set W of vectors (such as Rⁿ), a subspace of W is any
subset 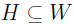satisfying three properties.
a. The zero vector is in H
b. If 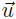and 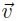are in H, then 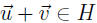. (We say H is closed under addition).
c. If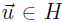, then for all scalar constants c, the vector 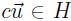. (We say H is
closed under scalar multiplication). Note. this includes c = 0 and c < 0.

Example 1. span of two vectors.
Say 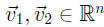, and H = Spanf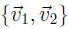. Then H is a subspace of Rⁿ.
Check.
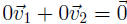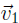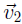a. is in the span of and , so .
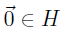b. If 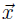and 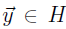, it means 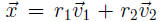and 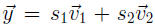for some
constants r₁, r₂, s₁, and s₂. Then,
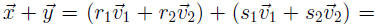
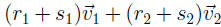, which is in H since it is a linear combination of 
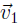
and 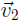(and therefore in the span of 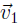and ).
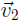c. If 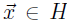, it means 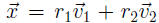for some constants r₁ and r₂. Then,
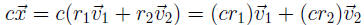which is in H.

Example 2. Line L in R² not through the origin.

Example III. The set
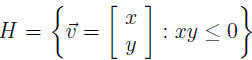. (Read the colon as "such that" or "satisfying".) Check the three properties.

Example IV. The set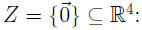

Definition. The column space of a matrix A (written "Col A") is the set of
all linear combinations of the columns of A, i.e. the span of the columns of A.

Definition. The null space of a matrix A (written "Nul A") is the set of all
solutions to the homogeneous equation

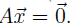
Theorem 12: For an m × n matrix A, the set H =Nul A is a subspace of Rⁿ.

Proof: Note. a vector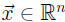 is in 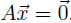by definition of this H.

Definition. A basis for a subspace H is a linearly independent set in H that
spans H.

Example V: The vectors 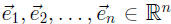are a basis for Rⁿ. In fact, they
are called the standard basis.

Example 6: Find a basis for the null space of the matrix

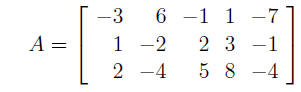
Write the solution to 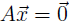in parametric vector form.

So x₂, x₄, and x₅ are free,

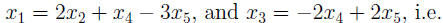
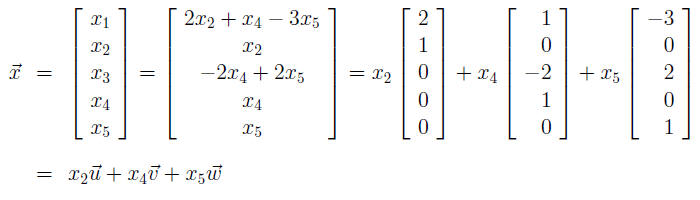
So Nul A =_____________________________

And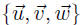 is a linearly independent set. So in fact it is a basis for Nul A.

This always happens, because.
1. When we write the solution set to 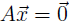in parametric vector form, the
solution set is always the set of all linear combinations of the vectors attached
to the free variables. That is, those vectors always span Nul A.
2. For a general matrix A and the equation 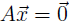, if x_i is a free variable,
think about the i^th position in each of the vectors in the parametric vector form
of the solution set to 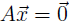. That position will be 1 in the vector which
goes with x_i, and will be 0 in all other vectors. The same holds for the other
free variables. So the only linear combination of those vectors which gives
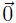
will be the trivial linear combination, i.e. the vectors will always be linearly
independent.

Result 1:To find a basis for the null space of A, write the solution set to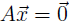 in parametric vector form. The vectors in that form are a basis.

Finding a basis for the column space of A takes less work, but some explanation
for why the technique works.
Example 7: Find a basis for the column space of the matrix

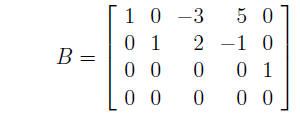
Calling the columns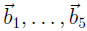 note that
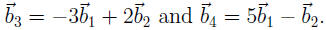
So any linear combination

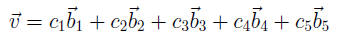
can really be written as

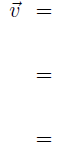
So in fact 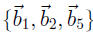spans Col B. Also, the set 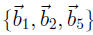is linearly indepen-
dent because those vectors are in fact the vectors 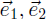, and 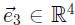which is
clearly a linearly independent set.

Since 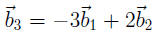, this also means that 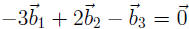 . This in turn
implies that

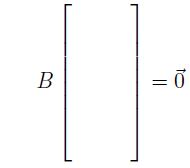
Now consider the matrix

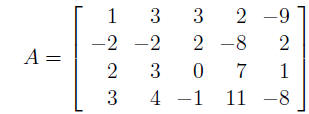
If you check, you will find that A is row equivalent to B on the previous page.
In fact, B = rref(A). The fact that A and B are row equivalent means that

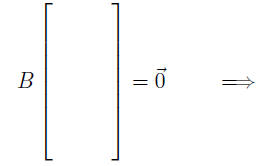
This in turn means that 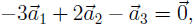 where 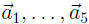are the columns
of A. So the same tricks we used with B will work for A, and in fact
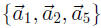
spans Col A.

Also 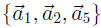is a linearly independent set (you still need to give it a little
bit of thought to fill in the details to see this).