Trigonometry
I. Course Objectives
Study of Degree Radian measure; right and oblique triangles; vector
applications; graph of
trig functions; graph of inverse trig functions; identities; conditional trig
equations; inverse
function; and unit circle.
II. Topics to Be Studied
How will course objectives be met?
I. Review of Algebraic Concepts
Real numbers
Directed lines and segments
Distance formula
Functions and graphs
II. The Trigonometric Functions
Angles and units of measure
Definition of sine, cosine and tangent, (ie sin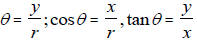
Cosecant, secant and cotangent functions as reciprocals
Value, the trigonometric functions for special angles (30•,• 60•,•45•,•
quadrantal angles)
Circular definition of the trigonometric functions (ie, the wrapping function)
III. Triangle and Tables of Trigonometric Functions
Interpolation - Students may use a calculator to solve the triangle problems
Right triangle problems
Applications of right triangles
Oblique triangles
Ambiguous case
Law of sines and law of cosines
IV. Vectors and Applications
Introduction - components and resolution
Applications - Inclined plane
Equilibrium - wind velocity and displacement aboard ships and airplanes
V. Trigonometric Identities
Ratio identities - Pathogren identities and reciprocal identities
Proving identities
Cosine, sine and tangent of the sum and difference of two angles
Double angle formulas
Half angle formulas
Product and sum formulas
Students are expected to be able to solve a large assortment of trig identities
VI. Graphical Representation of the Trigonometric Functions
Periods of trigonometric functions
Graph the trigonometric functions
Graphing general cases: y = A sin (Bx + C), y = A cos(Bx + C), y = A tan(Bx +
C),
y = A cot(Bx + C), y = A sec(Bx + C) and y = A csc(Bx + C)
VII. Trigonometric Equations and Inverse Functions
Solving conditional trigonometric equations
Inverse of a function
Inverse of the trigonometric functions
Solving inverse trigonometric equations
VIII. Optional Topics
Graphing y = A sin(Bx + C) + D cos(Ex + F) by addition of ordinates
The Scaler (inner product)
Complex Numbers
Logaritims of Trigonometric Functions
Area of triangle
S = bc sin A
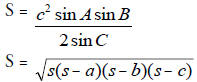
III. Special Projects to Be Included in Course
Research papers
Surveys
Other
Reports
Annotated bibliographies
IV. Methods of Student Evaluation
Tests (how many? how often? what type?)
Quizzes
Oral Presentations
Written Papers
Laboratory Activities
Clinical Experiences
3 to 6 Exams - scheduled throughout the semester
Objective Exams
Comprehensive Final Exam
V. Assessment of Outcomes
What measurements will be used to demonstrate that outcomes have been reached?
(Refers to class as a whole, not individual students.)
VI. Other Information
What additional information will help to clarify the course?
Prerequisites: Math 114, or consent of instructor, or satisfactory score on Math
Form C
Placement test, Reading 079

