Math 75 Notes

Proposition 1. The only units in F[x] are the nonzero constants in F.
The proof is simple: Suppose that A is an element of F[x] that has an inverse. Write

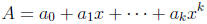
where we assume that 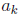is nonzero in F. If A has an inverse, then AB = 1 for some polynomial
B ∈ F[x]. Write

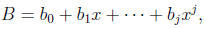
where 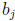is nonzero. In the product AB, the term 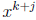shows up with a coefficient 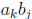of F,
and one can show (homework!) that 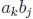is nonzero since both 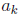and 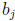are. So AB has degree
k + j. But we were supposed to have that AB = 1. Thus we need k + j = deg 1 = 0, which
means that k = j = 0, and so both A and B are constant polynomials.

The proposition tells us that we will have to do quite a bit more work to get the fields we
are after: starting with F and forming F[x] didn't give us any invertible elements.

Our approach will be the same as the approach taken in elementary number theory to
constructing the systems Z/(m). That approach begins with defining the notion of congruence
modulo m. In analogy, we make the following definition: We call two polynomials A,B ∈ F[x]
congruent modulo M if M divides A - B, i.e., if there is a polynomial Q ∈ F[x] for which

A - B = MQ:

In this case we write

A ≡ B (mod M):

For example, if F = Z/(2), then x³ ≡ x² + x + 1 (mod x + 1) in F[x], because x + 1 divides
the difference x³ -(x² +x+1) = x³ +x² +x+1 ∈ F[x]. (One can check this with the familiar
polynomial long division algorithm.)

If F is a field and M is a polynomial in F[x], then congruence modulo M is an equivalence
relation. In other words, this relation is...

• reflexive: A ≡ A (mod M) for every A,

• symmetric: if A ≡ B (mod M), then B ≡ A (mod M),

• transitive: if A ≡B (mod M) and B ≡ C (mod M), then A ≡ C (mod M).

Because of this, the ring F[x] is partitioned into equivalence classes. We define F[x]/(M) as
the set of equivalence classes. For each A ∈ F[x], denote the equivalence class containing A by
[A]; then

[A] := {B ∈ F[x] : B ≡ A (mod M)};

and F[x]/(M) is exactly the set of these classes [A] as A ranges over F[x].

The systems F[x]/(M) will be our candidates for new fields. For this to make any sense at
all, we need to define what it means to add and multiply two elements of F[x]. We make the
only definition that really is sensible: we define

[A] + [B] = [A + B]; and [A] · [B] = [AB]:

There is something to check here. The de nition of addition we've given here basically says `to
add two equivalence classes, pick an element from each, add those two elements, and then take
the equivalence class of the sum,' and similarly for multiplication. It is maybe not so obvious
that no matter how the elements are chosen, one always winds up with the same result. This
is a consequence of the fact that addition and multiplication respect congruence: if A₁ ≡ A₂
(mod M) and B₁ ≡ B₂ (mod M), then

A₁ + A₂ ≡ B₁ + B₂ (mod M); and A₁A₂ ≡ B₁B₂ (mod M):

We omit the (pretty easy) proofs of these facts here.

Let us do some examples to get a feel for the arithmetic of the systems F[x]/(M). For the
rest of this lecture we take F = Z/(5) and M = x² + 1 ∈ F[x], and we try to understand the
system F[x]/(M).

First let us see if we can do some basic arithmetic. Consider the two elements [x + 1] and
[x + 3] in F[x]/(M). By definition,

[x + 1] + [x + 3] = [(x + 1) + (x + 3)] = [(2x + 4)];

and

[x + 1][x + 3] = [(x + 1)(x + 3)] = [(x² + 4x + 3)]:

Actually the latter answer can be put in a somewhat simpler form. We have

[x² + 4x + 3] = [x² + 1 + 4x + 2] = [x² + 1] + [4x + 2] = [0] + [4x + 2] = [4x + 2]:

(This calculation of reduction should be viewed as being totally analogous to (say) the calcu-
lation that 3 · 5 = 15 = 8 in the system Z/(7).) It is somewhat cumbersome to keep having to
write these brackets, and so we omit them when the system we are working with is understood.
So, for example, in the future we will just write

(x + 1)(x + 3) = 4x + 2

when we are understood to be working in F[x]/(M) for F = Z/(5) and M = x² + 1.

How many elements are in our system F[x]/(M)? To answer this question it would be good
if we had a way of telling when two elements are different. For example, which elements of the
list

0, 1, x, 2x + 2, 3x³ + 2, x⁵

represent distinct elements of F[x]/(M)? We can get some insight into this question if we recall
that M = x² + 1 is zero in F[x]/(M). So

3x³ + 2 = 3x · x² + 2 = 3x(-1) + 2 = -3x + 2 = 2x + 2

and

x⁵ = x · (x²)² = x · (-1)² = x:

In fact, it's not hard to see that by repeatedly applying the rule that x² = -1, we can show
that every element of F[x]/(M) has the form a + bx, where a and b belong to F = Z/(5).

An alternative proof (which gets this result in one fell swoop) is to use long division for
polynomials. That process provides a constructive proof of the following fundamental result:

Theorem 3. Let F be a field. Let A,B be elements of F[x], and suppose B ≠ 0. Then there
are Q,R ∈ F[x] with

A = BQ + R with R = 0 or degR < degB:

Taking B = M, this result shows immediately that every polynomial is congruent to some
polynomial which is either zero, or of degree smaller than that of M. In our case, where
F = Z/(5) and M = x² + 1, that means that very equivalence class is represented by a
polynomial either zero or of degree < 2. Again, these are precisely the polynomials of the form
a + bx.

At this point it is tempting to assert that F[x]/(M) has precisely 5 · 5 = 25 elements: there
are 5 choices of a and 5 choices for b. But perhaps there is some repetition even among the
elements a+bx? It seems hard to see how this could occur, since the rule x² = -1 that defines
the system F[x]/(M) doesn't seem to imply any such coincidences. We now prove that all the
elements a + bx, with a,b ∈ F = Z/(5), do define distinct elements of F[x]/(M), so that our
system does have 25 elements as claimed. For the proof, notice that if

a + bx = a' + b'x

for a, b, a', b' ∈ F, then

(a - a') + (b - b')x = 0:

Expressed in the language of congruence, this asserts that

a - a' + (b - b')x ≡ 0 (mod x² + 1);

i.e., that

(a - a') + (b - b')x = (x² + 1)Q(x)

for some polynomial Q(x) ∈ F[x]. But if Q(x) is nonzero, then the degrees of the left and right
hand sides will not match up! So it must be that Q(x) = 0, which implies that a-a'+(b-b')x =
0, which in turn implies that a = a' and b = b'.

The proofs we have just outlined work in general. The corresponding result is as follows:

Theorem 4. Let F be a finite field. Let M be a nonzero polynomial in F[x]. Then the number
of elements in F[x]=(M) is 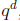, where q is the number of elements of F and d is the degree of
M. In fact, every element of F[x]/(M) has the form

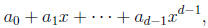
where 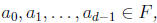and the 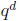elements de fined this way are all distinct.