Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

2.1 - Matrix Operations

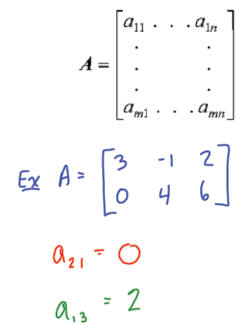
•Denoting a general matrix A of m rows and n columns

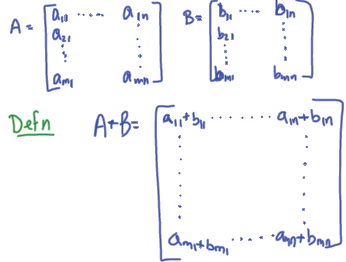
Adding matrices, multiplying by scalars

Example:

•So matrix addition and scalar multiplication are component‐wise.
•Exercise: Write a sum of two general matrices A, B

Properties of Addition & Scalar Mult

• If A, B, C are the same size, r, s any scalars,
then
• A+ B=B+ A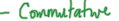
• (A+ B) +C=A+ (B+C)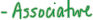
• A+0=A if 0 is the matrix of the same size, consisting
of all 0’s
•Other facts on p 108, Th 1

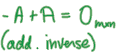
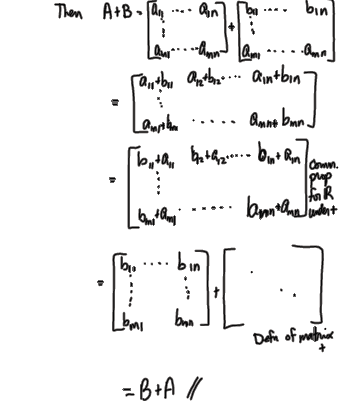
How to write a proof of a matrix fact

•Commutative property (A+ B=B+ A)

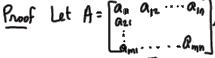
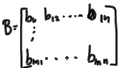
Matrix Multiplication

• We have already seen when we can multiply AB.
• Review how it works

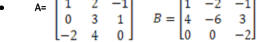
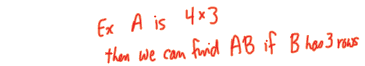
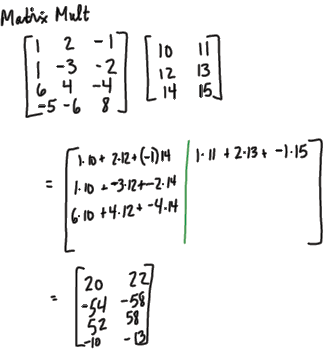
Matrix Multiplication – General Case

•Use the columns of B
(In text)

•General rule (without columns) – p 111

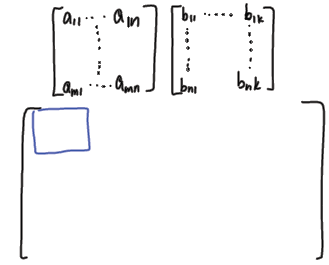
Computing a specific row/column of a product

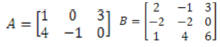
· Find

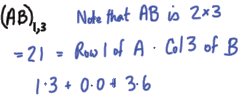
Properties of Matrix Multiplication

•P 113, Th 2
•Associative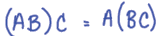
•Left Distributive
•Right Distributive
•Scalar multiples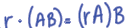
• Identity
•Note what’s missing! Verify.

Transpose A^T

• Definition

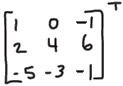
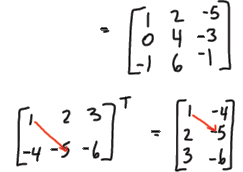
Properties of A^T
•Page 115 (Th 3)

A+ Algebra Resources

We will end your math anxiety

2.1 - Matrix Operations

More Tutorials