Rational Functions

What if instead of looking at the limit of x, we look at the limits of a, b, c, and d in relation to our function?

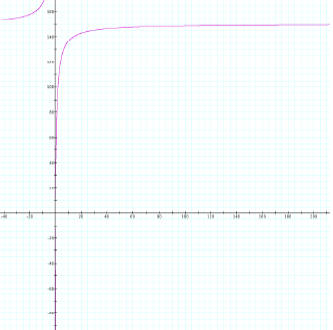
Limit of a (towards infinity):

As the limit of approaches infinity the right hand limit approaches negative infinity and left hand limit of f(x)
approaches infinity. This happens very quickly. Below is a graph illustrating this idea. Here, b, c, and d= 1
and n=150. While this isn’t showing a=infinity we can generalize the idea.

We also know f(x) cannot exceed the value of infinity since a horizontal asymptote exists at a.

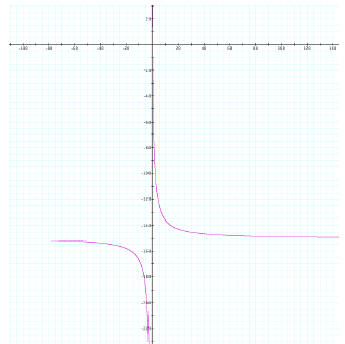
Limit of a (towards negative infinity):

Here as approaches infinity the left hand limit approaches negative infinity and right hand limit of f(x)
approach infinity. Once again, a graph is used to illustrate this point (a=-150, b=1, c=1, d=1). In this case,
the function approaches negative infinity rather quickly. Additionally we know that the limit of f(x) does
not go past negative infinity since a horizontal asymptote exists at a.

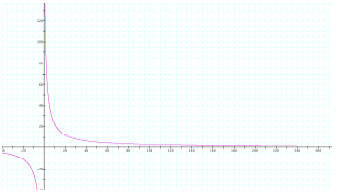
Limit of b (towards infinity and negative infinity):

Here I looked at what happens to the function f(x) if the limit of b is examined. First, we can see that as b
goes towards infinity, the right hand limit of f(x) goes towards infinity and the left hand limit goes towards
negative infinity. Also, if b goes towards negative infinity, the right hand limit f(x) goes towards negative
infinity and the left hand limit goes towards positive infinity.

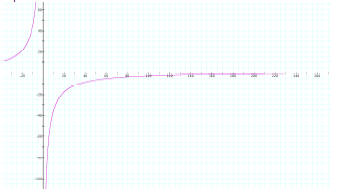
The first graph shows f(x) with a=230, b=1, c=1, and d=1 to illustrate what happens when b goes towards
infinity. The second graph shows f(x) with a=-390, b=1, c=1, and d=1.

Graph #1

Graph #2

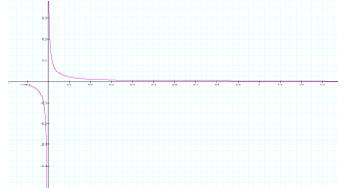
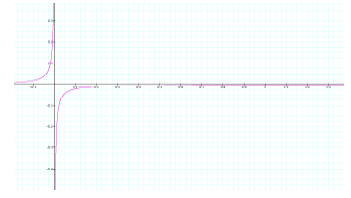
Limit of c (towards infinity and negative infinity):

Here when c approaches infinity the limit of f(x) approaches 0. We can see this illustrated through graphs
by observing what happens when c=500, and if we let a, b, and d remain as fixed values. When this
happens, the limit of f(x) approaches 0 from both sides. This is also true if we allow c to approach negative
infinity. In the second graph I allowed c=-500 to illustrate this point.

Graph #1

Graph #2

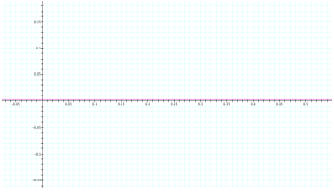
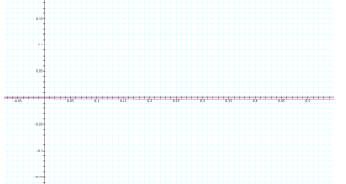
Limit of d (towards positive and negative infinity): When a, b, and c remain fixed and d approaches positive
or negative infinity, the limit of f(x) approaches 0. The first graph illustrates this point by showing d=500,
a=1, b=1, and c=1. The second graph shows that this also occurs when d approaches negative infinity,
where d=-500, a=1, b=1, and c=1.

Graph #1

Graph #2

Final thoughts on a, b, c, and d:

It makes sense algebraically that as a and b approach infinity the limit f(x) goes towards infinity and as a
and b approach negative infinity the limit of f(x) goes towards negative infinity.

For instance, if we are looking at a going towards infinity and b, c, and d are fixed and c and d are even
some large values (c=500, and d=1000) and b=1…we are still approaching infinity...

Why?

Because numbers such as 9,999,999,999,999,999,999. . . are extremely large in comparison to numbers
such as 500 and 1000.

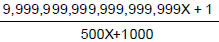
= A very large number!

*Also, as a continues to increase the limit of f(x) approaches infinity. The same idea holds for negative
infinity (except we are approaching negative infinity) and if we manipulate b instead of a.

For c and d, it makes sense that as c or d approaches infinity or negative infinity that we are approaching 0.
Why?

Well because as this happens we are essentially generating the value

f(x) = (1/9999999999999999999) or -(1/9999999999999999999) depending on whether or not c or d is
approaching positive or negative infinity. Either way, these values become increasingly smaller and smaller
as c and d go towards positive or negative infinity. Eventually, they are so small that they essentially equal
0.

Mathematical Foci 5: Inverse of f(x)
Inverse of the function f(x) = (ax + b) / (cx + d)

Definition:
A function is said to be an inverse of a given function if the domain and the range trade places. The
elements of the domain become range and vis-à-vis.

The given function is: ƒ(x) = (ax + b) / (cx + d)
The inverse of the function is: ƒ^-1 (x) = (dx –b) / (-cx + a).

Below is the explanation on how to solve for ƒ^-1 (x).

The inverse of the function ƒ(x) = ax + b/cx + d can be solved in several ways. Some of these are:

a) Algebraically:
Assuming f: R→R a function and f(x) = (ax + b/cx + d).
To find an inverse of a function we assume ƒ(x) = y = (ax + b/cx + d) then cross multiplying (cx + d) and y.
We will get cxy + dy = ax + b and if we transfer all the x’s in the same side then we get x(cy-a) =b – dy.
Dividing both side by (cy-a) then we get x = (b-dy)/(cy-a). Multiplying both side by -1 then we get x = (dy-b)/
(-cy+a). The last step is replacing y’s with x then we get ƒ^-1 (x) = y = (dx – b) / (-cx + a).

b) Using linear algebra method
Assume 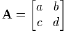is a 2x2 matrix and ad-bc ≠ 0. Multiplying this matrix by a 2x1 matrix, then we get
2x1 matrix A[x] =

To find the inverse of A[x] = we must define identity matrix. Identity matrix is denoted by Ι.

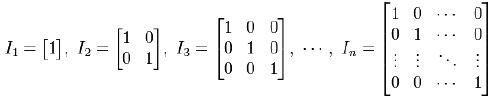
We denote the inverse of a 2X2 matrix 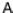is 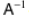such that,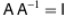. where I is identity matrix. Then the
inverse is

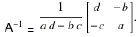where ad-bc ≠ o. If we assume ad-bc = 1 then 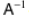[x] = .
The inverse of the function has something to say about the function itself. Here are some that we found out.

Take for example ƒ(x) = (2x+3)/(4x+5) and its inverse ƒ^-1 (x) = (5x-3)/(-4x+2). The graphs of the function
and its inverse are here below.

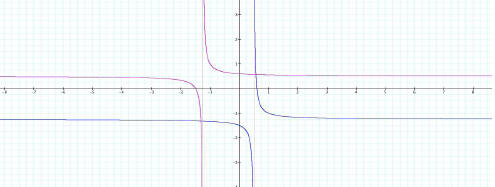
Graph 1

*ƒ(x) is in red while ƒ^-1 (x) is in blue.

To make a reasonable observation, the graphs below are presented. The same set of function and its
inverse is used. The value of b, c, and d are changed in graphs 2, 3, and 4 respectively.

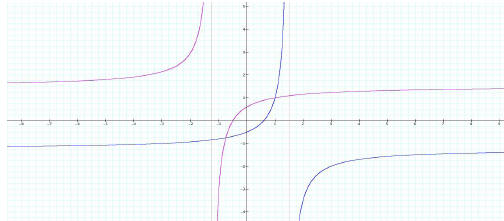
Graph 2

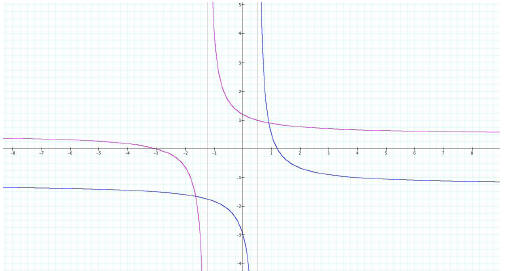
Graph 3

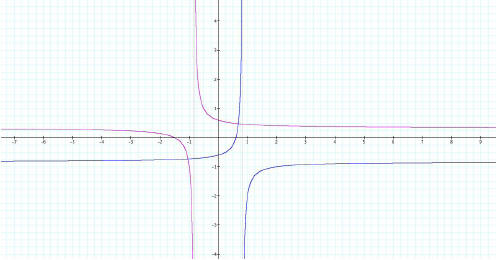
Graph 4

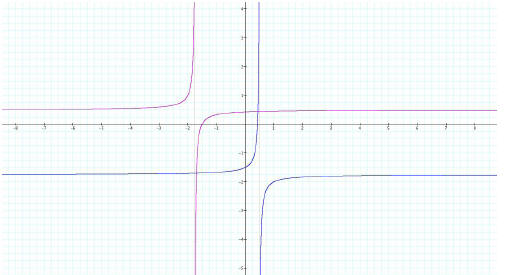
Graph 5

General observation:
The non-corresponding asymptotes of the graphs of the ƒ(x) and ƒ^-1 (x) are parallel. Furthermore, the graph
of ƒ^-1 (x) is reflected to the opposite direction of ƒ(x).