QUADRATIC FORMULA
HOW TO SOLVE ANY QUADRATIC EQUATION: First of all, make sure that you
know the
difference between a quadratic equation and The Quadratic Formula. A quadratic
equation is any equation
that is second degree. The Quadratic Formula is the formula used to solve any
quadratic equation. You
have probably heard of this formula, and some of you have probably already used
it. Actually any quadratic
equation can be solved by completing the square, but the Quadratic Formula gives
us a direct way to get
the solutions that is often quicker.
WHERE DOES IT COME FROM?: You are certainly NOT responsible for
deriving the Quadratic
Formula. I show the derivation here for those that are interested and so that
you are at least aware that it
is a direct consequence of Solving by Completing the Square, which in turn was
dependent upon Extracting
Roots. First: The equation must be set equal to 0.
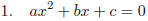 Start
with a general second degree equation equal to zero.
Start
with a general second degree equation equal to zero.
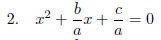 Divide
every term by a to get coefficient of x^2 to be 1, & keep equation equivalent.
Divide
every term by a to get coefficient of x^2 to be 1, & keep equation equivalent.
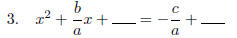 Move
constant to RIGHT & set up blanks for Completing the Square.
Move
constant to RIGHT & set up blanks for Completing the Square.
Now figure out what has to be added: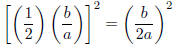
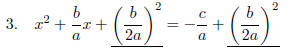 LEFT
side is now a Perfect Square Trinomial
LEFT
side is now a Perfect Square Trinomial
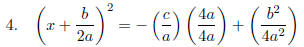 LEFT
- Binomial Squared; RIGHT - Common denominator:
LEFT
- Binomial Squared; RIGHT - Common denominator:
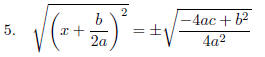 Extract
Roots after combining RIGHT to one fraction.
Extract
Roots after combining RIGHT to one fraction.
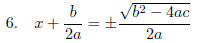 “Rearrange”
numerator terms & simplify square root of denominator.
“Rearrange”
numerator terms & simplify square root of denominator.
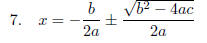 Isolate
x
Isolate
x
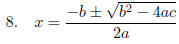 Add
fractions together, using common denominator, 2a.
Add
fractions together, using common denominator, 2a.
QUADRATIC FORMULA: Here it is:
IF ax^2 + bx + c = 0 THEN:
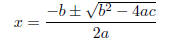 Gives the solutions for x to the above equation.
Gives the solutions for x to the above equation.
REMEMBER: The equation MUST start set equal to 0 before using the formula!
ALSO: Notice the position of the fraction bar under the entire numerator. Please
be NEAT & CAREFUL
about this placement!
DO I HAVE TO MEMORIZE IT?: YES! Rather, I hope you will LEARN it from
practicing.
But that is the BEST way to learn it is to PRACTICE, PRACTICE, PRACTICE, · · ·.
Furthermore, just
“substituting” the correct numbers into the correct formula is only about HALF
the problem. You must
know how to correctly SIMPLIFY what you get.
EXAMPLE: SOLVE using the Quadratic Formula:
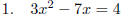 FIRST
the equation MUST be set equal to 0 before the Formula can be applied:
FIRST
the equation MUST be set equal to 0 before the Formula can be applied:
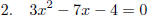 NOW
determine: a = 3, b = −7, c = −4. Watch your signs.
NOW
determine: a = 3, b = −7, c = −4. Watch your signs.
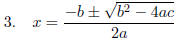 To
learn quickly, WRITE and SAY the Formula each time.
To
learn quickly, WRITE and SAY the Formula each time.
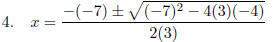 SHOW
your substitution step.
SHOW
your substitution step.
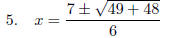 Proceed
with the Arithmetic.
Proceed
with the Arithmetic.
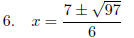 This
one required little simplification.
This
one required little simplification.
WARNING: Notice in Step 1, that the correct substitution for b2 = (−7)2 NOT −72.
Remember our
discussion in class as to Order of Operations: −72 = −49. If you wirte −72 and
then 49 in the next
step, you have made two errors!
NEXT EXAMPLE: SOLVE using the Quadratic Formula:
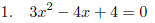 IS set equal to 0
ready for the Formula, with a = 3, b = −4, c = 4.
IS set equal to 0
ready for the Formula, with a = 3, b = −4, c = 4.
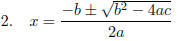 WRITE and SAY the
Formula.
WRITE and SAY the
Formula.
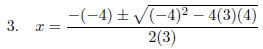 SHOW your substitution
step.
SHOW your substitution
step.
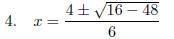 Proceed with the
Arithmetic.
Proceed with the
Arithmetic.
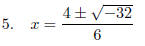
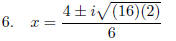 “Take i out”
“Take i out”
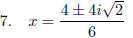 Simplify Radical (You
can combine last two steps easily.)
Simplify Radical (You
can combine last two steps easily.)
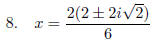 Factor a 2 out of
numerator to cancel with denominator:
Factor a 2 out of
numerator to cancel with denominator:
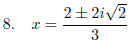 So you can see on a
problem like this that the substitution was just the beginning!
So you can see on a
problem like this that the substitution was just the beginning!
WARNING: One of the MOST common MISTAKES is “cancelling”
an “added term” from the numerator
in one of the last steps. This would be a VSE - Very Serious Error - DON’T DO
IT!
NOTE: I have NO problem with you combining some steps. I
tried to put in everything in these examples.
I will ask you to SHOW your SUBSTITUTION STEP, so that I know that you are doing
this correctly,
and to discern where possible errors are coming from. After that you may combine
some steps, but on a
problem as long as this last one, I would doubt that anyone would do all the
steps in their head, so put down
the steps that you need, rather than working it on scratch paper and just giving
me an answer - UNacceptable!
LAST EXAMPLE: SOLVE using the Quadratic Formula:
1. x2 + 5x + 6 = 0 IS set equal to 0 ready for the Formula, with a = 1, b = 5, c = 6.
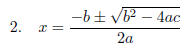 WRITE and SAY the
Formula.
WRITE and SAY the
Formula.
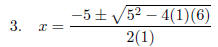 SHOW your substitution
step.
SHOW your substitution
step.
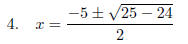 Proceed with the
Arithmetic.
Proceed with the
Arithmetic.
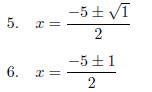
Now this serves to illustrate what must be done when the
radical “comes out even”. It would not be
proper to leave the answer in this form because the two individual answers:
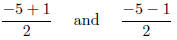 simplify to two other
numbers:
simplify to two other
numbers: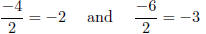 respectively.
respectively.
7. x = −2 or x = −3 Answers correctly simplified.
Actually, if you had just been asked to SOLVE this
equation any way you wanted to, you would have
factored one this simple; however, I used this to illustrate that when you do
use the Quadratic Formula, or
Solve by Completing the Square, or by Extracting Roots and the solution comes
out with NO Radical left,
you MUST simplify the two numbers individually, rather than leave it in “±
notation.”

