Tips for Establishing Trigonometric Identities
Getting Started:
1. Start by determining which side of the identity is
simpler and which side is more complicated. Rewrite the identity with the
simpler side on the left and the more complicated side on the right. We will
establisha trigonometric identity by working the right–hand side until it looks
like the left. (Occasionally we may have to work the left side a little so that
we can make sure both sides match.)
2. On both sides of the equation express tanθ. , cscθ. , secθ. , and cotθ. in
terms of sinθ. and cosθ.
Algebraic Steps to Consider:
1. Look at the number of terms on both sides, then
determine if you need to combine fractions or break up fractions so that the
number of terms will match.
· Combine two or more fractions over a common denominator to produce a
single fraction.
· Split up a single fraction with two or more terms in the numerator by
putting each term in the numerator over the common denominator.
2. Multiply the numerator and denominator of a fraction by a form of the number
“1”.
· For complex fractions multiply both the numerator and denominator by
the LCD to clear fractions.
· To match on a particular denominator you may need to multiply both the
numerator and denominator by the denominator you are trying to get.
· To rationalize the denominator, multiply both the numerator and
denominator by the conjugate of the denominator
· Multiply by either the conjugate of the numerator or denominator to get
a Difference of Squares, so that we can use a Pythagorean Identity.
3. Expand expressions by multiplication, if possible , then combine like terms
and simplify.
· Expand a Binomial Squared. (a ± b)^2 = a^2 ± 2ab + b^2
· Expand the Product of a Sum and Difference of Two Terms. (a +b)(a -b)
=a^2 -b^2
4. Factor the numerator and denominator, if possible, to cancel common factors
taking the fraction to lowest terms .
· Factor out the Greatest Common Factor.
· Factor a Difference of Squares. a^2 - b^2 = (a + b)(a - b)
· Factor a Sum/Difference of Cubes. a^3 ± b^3 = (a± b)(a^2
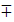ab + b^2 )
5. Recognize patterns from Identities and Formulas.
· Reciprocal, Quotient, Pythagorean, and Even/Odd Identities.
· Sum and Difference Formulas.
· Double/Half Angle Formulas and Power Reducing Formulas.
· Product–to–Sum and Sum–to–Product Formulas.
Knowing Which Formula to Use:
1. There are no formulas (except Pythagorean Identities)
involving cscθ , secθ , and cotθ . If you are given one of these three functions
apply a ReciprocalIdentity then decide what to do next.
2. If the angle is…
 |
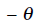use | Even–Odd Identities |
 |
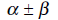use | Sum and Difference Formulas |
 |
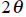use | Double Angle Formulas |
 |
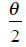use | Half Angle Formulas |
3. If you have …
 |
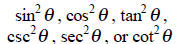use | Pythagorean Identities or a Power Reducing Formula |
 |
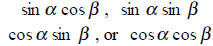use | Product–to–Sum Formulas |
 |
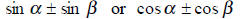use | Sum–to–Product Formulas |
