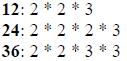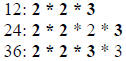Greatest Common Factor
Factors shared by two or more whole numbers are
called common factors. The largest
of the common factors is called the Greatest Common Factor (GCF). There
are three
methods we will be learning.
List the Factors. Method 1.
Ex.
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Look to see what factors that both 24 and 36 share. They share 1,2,3,4,6, and
12. The
Greatest factor is 12. So the Greatest Common Factor or GCF is 12.
Sometimes you come across large numbers and it is hard to find all the common
factors.
Use Prime Factorization. Method 2.
| Ex.
|
I have Bolded the common factors.
|
So now we look at the prime numbers they all have in
common. They have a 2, and
another 2 and a 3. So they Share 2*2*3. We need to multiply these together to
get the
GDF. 2*2*3=12.
GCF: 12
There is another way to look at finding GCF. Using the Ladder Method. Method 3.
This is similar to using division, but we only divide by prime numbers.
We will use the same example as the one above to show that it doesn’t matter
what
method you use you get the same answer.
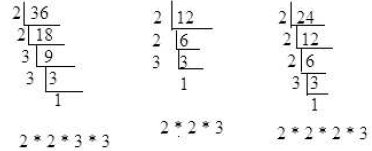
| You can see what they all share: 36: 2 * 2 * 3 * 3 24: 2 * 2 * 2 * 3 12: 2 * 2 * 3 Share: 2* 2 * 3 = 12 GCF: 12 |
You can use any method you wish, BUT use the same method
for the entire
problem. DO NOT mix methods within one problem. You may choose
other methods for different problems.
Find the GCF of these problems:
1. 60 and 84
2. 14 and 17
3. 10, 35 and 110
4. 21 and 306
5. 630 and 712
6. 75, 225, and 150
7. 16, 24,30 and 42
8. 2x2x3 and 2x2