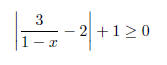Math 111 Final Exam Review
Chapter 3
3.1: Functions
You need to know the definition of a function. You need to
know when an equation in two variables
describes one variable as a function of the other variable.
11. State the definition of function.
12. True/False. The equation 3y^2 − x^3 = 3 describes x as a function of y.
3.2: Functional Notation
You need to be comfortable with function notation,
piecewise defined functions, and reading graphs
of functions. You need to be able to compute the difference quotient (The
formula for the difference
quotient will be on the exam). You need to be able to determine the domain of
functions.
13. True/False. For all functions f, with a, b in the domain of f, f(a) − f(b) = f(a − b).
14. Determine the difference quotient of f(x) = 4x^2 − 2x + 1.
15. True/False. The domain of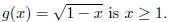
16. Determine the domain of the function below.
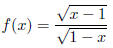
3.3: Graphs of Functions
From 3.3, you should know the graphs of the “Catalog of
Basic Functions” on page 170. You should
know what local maxima and local minima means, and you should be familiar with
the vertical line
test and what it tells you. You should be able to interpret the graph of a
function.
3.4: Graphs and Transformations and 3.4A: Symmetry
From 3.3: You need to understand horizontal shifts (f(x−c)
shifts the graph of f c units to the right),
vertical shifts (f(x) + c shifts the graph of f c units up), and reflections
(f(−x) is a reflection across
the y-axis, −f(x) is a reflection across the x-axis).
17. The graph of f is given below. Sketch the graph of f(−x) + 3.
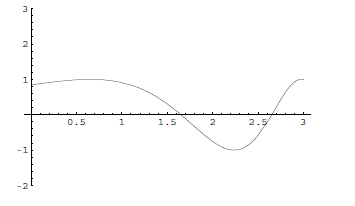
From 3.4A: You need to know what it means for the graph of
an equation to be symmetric with respect
to the x-axis, symmetric with respect to the y-axis, and symmetric with respect
to the origin, and be
able to determine this algebraically. You need to know when a function is even,
odd, or neither, and
how to determine this algebraically.
18. Determine whether the graph of the equation 4y^2 +
3x^3 = x is symmetric with respect to the y-axis,
x-axis, and/or origin.
19. Determine whether the function below is even, odd, or neither.
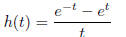
3.5: Operations on Functions
You need to be able to determine the rules and domains of
functions obtained by adding, subtracting,
multiplying, dividing, and composing two functions.
20. Let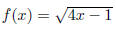 and
and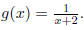 Determine
the domain of fg and
Determine
the domain of fg and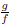
21. Let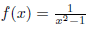 and
and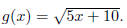 Determine
the rule and domain of
Determine
the rule and domain of 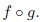
3.7: Inverse Functions
You need to know when a function has an inverse, and how
to use the horizontal line test to determine
whether a function has an inverse. You should know the properties of inverse
functions. You should
be able to determine the inverse of a function algebraically. You should know
the round trip theorem.
You need to know the properties of graphs of inverse functions.
22. Write down the Factor Theorem.
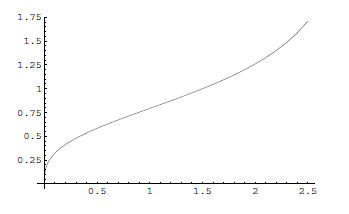
23. Find the inverse function to
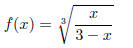
24. Sketch the graph of the inverse function to the function given below on the same axes.
Chapter 4
4.1: Quadratic Functions
The important idea from this section was finding the
vertex of a parabola. You need to be able to do
this, and also be able to do word problems involving finding the vertex of a
parabola.
25. Find the vertex of the graph of the following quadratic equation.
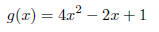
26. In Lawrence, Kansas, there is a city ordinance stating
that as you enter the city, you must fire your
gun into the air to alert the inhabitants of your presence. Cletus drives into
Lawrence and fires his
rifle into the air. The bullet follows a trajectory given by the following
equation:
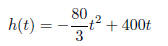
Where h is the height in feet above the ground, and t is
the time (in seconds) after Cletus fires his
gun. What is the maximum height the bullet reaches? How many seconds after
Cletus fires his gun
will the bullet reach the ground?
27. The profit of Weber Vacuum Company is given by the following quadratic equation:
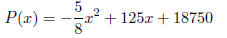
where P is the profit in USD, and x is the number of
Vacuums sold. What is the maximum profit
Weber Vacuum Company can make, and how many vacuums should they sell to make
this profit? If
the Weber Vacuum Company sells enough vacuums, they will make no profit. How
many vacuums do
they need to sell for this to occur?
4.2: Polynomial Functions
The division algorithm, factor theorem, and remainder
theorem are important. You should know how
to divide polynomials.
28. State the Factor Theorem
29. State the Remainder Theorem.
30. True/False. x − 1 is a factor of x^99 − x^22 + x^45 + 1.
31. What is the remainder when x^6 − x^5 + x^4 − x^3 + x^2 − x + 2 is divided by x − 2?
4.4: Graphs of Polynomial Functions
You should know how the multiplicity of a root affects the
x-intercept of the graph. You should know
that the graph of a polynomial function of degree n has at most n x-intercepts
and n−1 local extrema.
You should know how the degree of a polynomial affects the behavior of the graph
when |x| is large.
Given a graph of a polynomial, you should be able to determine whether the
polynomial could have a
certain degree.
32. True/False. A polynomial of degree 5 can have 5 x-intercepts.
33. True/False. The polynomial function whose graph is given below could have degree 3.
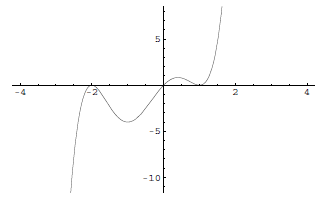
34. Give an example of a polynomial function of degree 5 with only one root.
4.5: Rational Functions
You need to be able to determine the domain, x-intercepts,
y-intercepts, vertical asymptotes, holes,
and horizontal asymptotes of rational functions.
35. True/False: The domain of
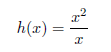
is 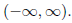
36. Find the domain, x-intercepts, y-intercept, vertical
asymptotes, holes, and horizontal asymptotes of
the following rational function.
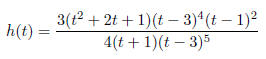
37. Find the domain, x-intercepts, y-intercept, vertical
asymptotes, holes, and horizontal asymptotes of
the following rational function.
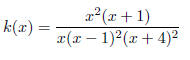
4.6A: Absolute Value Inequalities
You should be able to solve simple absolute value inequalities.
38. Find all solutions to
|5x − 1| > 5
39. Find all solutions to
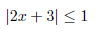
40. Determine the solutions to