Fractions, Decimals, and the Volume of a Sphere
1. Converting Fractions to Decimals: To convert a
fraction to a
decimal, divide the numerator by the denominator. You must divide
until the decimal terminates or repeats unless the instructions ask you
to round to a given decimal place.
Example 1: Convert the given fraction to a decimal.
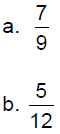
Example 2: Convert the given fraction to a decimal. Round
to
the nearest thousandth, if necessary.
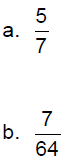
2. Converting Decimals to Fractions: To convert a
decimal to a
fraction,
• Numerator of the fraction: Place the digits to the right of
the decimal point.
• Denominator of the fraction: Write the place value named
by the last digit in the decimal if the “ths’ is left off.
• Reduce the fraction to lowest terms.
Example 3: Convert to a fraction in lowest terms.
a. 3.045
b. 2.125
3. Problems Containing Both Fractions and Decimals: To work
problems that have both fractions and decimals, you may
• Change all of the decimals to fractions and simplify.
• Change the fractions to decimals, if they make terminating
decimals, and then simplify. If the fractions do not make
terminating decimals, don’t use this technique.
• Try to divide out any common factors, and then simplify.
Common factors can be divided out even when one or both of the
numbers are decimals.
Example 4 :
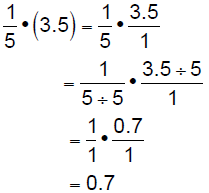
Example 5: Simplify by dividing out common factors. Give
an
exact answer; that is, do not round.
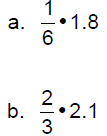
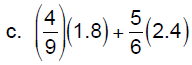
Sometimes, there are no common factors to divide out or it
is simply
easier to convert the fractions to decimals and complete the
arithmetic. As long as the fractions convert to terminating decimals,
this technique will work well. However, if the problem contains
fractions that convert to repeating decimals, then you will introduce
error in the answer when you round that decimal in order to do the
remaining calculations. These problems are best done by calculator
where the calculator can carry 15 or more decimal places, minimizing
the error in the answer.
Try these problems. If the problem contains a fraction that converts
to a repeating decimal, use a calculator and round your answer to the
nearest hundredth.
Example 6: Simplify.
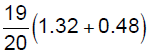
Example 7: Simplify. Round your answer to the nearest
hundredth.
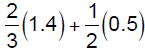
5. Volume of a sphere: The volume of a
sphere of radius r is given
by
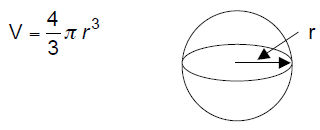
To solve these geometry problems, remember to write out
the
following steps:
• Write the formula,
• Plug in the known values using 3.14 for π, and
• Use your calculator to complete the calculations and write
your answer with the correct units. Round to the nearest
hundredth
Example 8: Find the volume of a sphere of radius 17.859 feet
Practice Problems:
a. Convert the given fraction to a decimal. Do not round.5/18
b. Convert the given fraction to a decimal. Round to the nearest
hundredth.5/17
c. Simplify. Give an exact answer.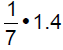
d. Simplify. Give an exact answer .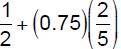
e. Simplify. Use a calculator and round your answer to the
nearest hundredth.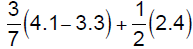
f. Find the volume of a sphere of diameter 23.45 yds. (Hint:
First find the radius of the sphere.)
Answers to Practice Problems:


