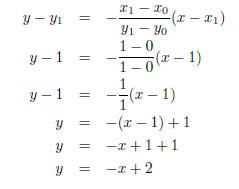Textbooks for High School Students Studying the Mathematics

42.3 Co-ordinate Geometry

42.3.1 Equation of a Circle
We know that every point on the circumference of a circle is the same distance away from the
centre of the circle. Consider a point (x₁,y₁) on the circumference of a circle of radius r with
centre at (x₀,y₀).

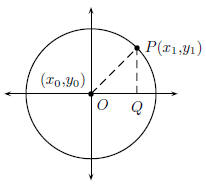
Figure 42.3: Circle h with centre (x₀,y₀) has a tangent, g passing through point P at (x₁,y₁).
Line f passes through the centre and point P.

In Figure 42.3, △OPQ is a right-angled triangle. Therefore, from the Theorem of Pythagoras,
we know that:
OP² = PQ² + OQ²

But,
PQ = y₁ - y₀
OQ = x₁ - x₀
OP = r
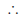r² = (y₁ - y₀)² + (x₁ - x₀)²

But, this same relation holds for any point P on the circumference. In fact, the relation holds
for all points P on the circumference. Therefore, we can write:
(x - x₀)² + (y - y₀)² = r²   (42.3)

for a circle with centre at (x₀,y₀) and radius r.

For example, the equation of a circle with centre (0,0) and radius 4 is:
(y - y₀)² + (x - x₀)² = r²
(y - 0)² + (x - 0)² = 4²
y² + x² = 16

Worked Example 192: Equation of a Circle I

Question: Find the equation of a circle (centre O) with a diameter between two
points, P at (-5,5) and Q at (5, - 5).

Answer
Step 1 : Draw a picture
Draw a picture of the situation to help you figure out what needs to be done.

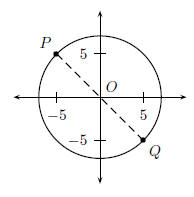
Step 2 : Find the centre of the circle

We know that the centre of a circle lies on the midpoint of a diameter. Therefore
the co-ordinates of the centre of the circle is found by finding the midpoint of the
line between P and Q. Let the co-ordinates of the centre of the circle be (x₀,y₀),
let the co-ordinates of P be (x₁,y₁) and let the co-ordinates of Q be (x₂,y₂). Then,
the co-ordinates of the midpoint are:

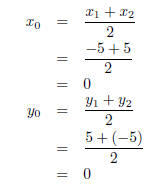
The centre point of line PQ and therefore the centre of the circle is at (0,0).
Step 3 : Find the radius of the circle
If P and Q are two points on a diameter, then the radius is half the distance between
them.
The distance between the two points is:

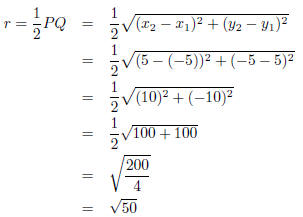
Step 4 : Write the equation of the circle
x² + y² = 50

Worked Example 193: Equation of a Circle II

Question: Find the center and radius of the circle
x² - 14x + y² + 4y = -28.

Answer
Step 1 : Change to standard form
We need to rewrite the equation in the form (x - x₀) + (y - y₀) = r²
To do this we need to complete the square
i.e. add and subtract ( 1/2 cooefficient of x)² and ( 1/2 cooefficient of y)²

Step 2 : Adding cooefficients
x² - 14x + y² + 4y = -28
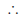x² - 14x + (7)² - (7)² + y² + 4y + (2)² - (2)² = -28
Step 3 : Complete the squares
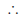(x - 7)² - (7)² + (y + 2)² - (2)² = -28
Step 4 : Take the constants to the other side
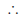(x - 7)² - 49 + (y + 2)² - 4 = -28
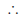(x - 7)² + (y + 2)² = -28 + 49 + 4
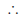(x - 7)² + (y + 2)² = 25
Step 5 : Read the values from the equation
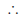center is (7;-2) and the radius is 5 units

42.3.2 Equation of a Tangent to a Circle at a Point on the Circle
We are given that a tangent to a circle is drawn through a point P with co-ordinates (x₁,y₁).
In this section, we find out how to determine the equation of that tangent.

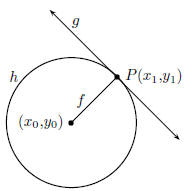
Figure 42.4: Circle h with centre (x₀,y₀) has a tangent, g passing through point P at (x₁,y₁).
Line f passes through the centre and point P.

We start by making a list of what we know:

1. We know that the equation of the circle with centre (x₀,y₀) is (x-x₀)² +(y -y₀)² = r².
2. We know that a tangent is perpendicular to the radius, drawn at the point of contact with
the circle.

As we have seen in earlier grades, there are two steps to determining the equation of a straight
line:
Step 1: Calculate the gradient of the line, m.
Step 2: Calculate the y-intercept of the line, c.

The same method is used to determine the equation of the tangent. First we need to find the
gradient of the tangent. We do this by finding the gradient of the line that passes through the
centre of the circle and point P (line f in Figure 42.4), because this line is a radius line and the
tangent is perpendicular to it.

The tangent (line g) is perpendicular to this line. Therefore,

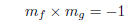
So,

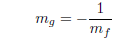
Now, we know that the tangent passes through (x₁,y₁) so the equation is given by:

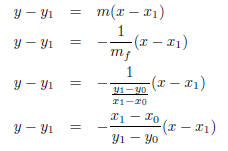
For example, find the equation of the tangent to the circle at point (1,1). The centre of the
circle is at (0,0). The equation of the circle is x² + y² = 2.
Use

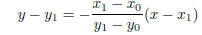
with (x₀,y₀) = (0,0) and (x₁,y₁) = (1,1).