Linear and Quadratic Functions

Section summaries

Section 4.1 Linear Functions and Their Properties

A linear function is one of the form

f(x) = mx + b ,

where m gives the slope of its graph, and b gives the y-intercept of its graph. The slope m
measures the rate of growth of the function, so a linear function is increasing if m > 0 and
decreasing if m < 0.

Review problems: p284 #17,21,25,37,43,49

Section 4.2 Building Linear Functions from Data

In this section linear functions are constructed from data presented in various ways.

Review problems: p290 #3,5,7,15,19,21

Section 4.3 Quadratic Functions and Their Properties

The general form of a quadratic function is



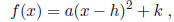
where (h, k) is the vertex of the graph (which is a parabola). You can see from the formula
that h gives the left/right shift while k gives the up/down shift. The coefficient a represents
a vertical stretch or compression. Since the basic member of this family is f(x) = x², whose
graph opens up, the graph of 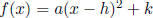  will open up if a is positive, and down
if a is negative. If the graph opens up, its height is minimum at the vertex, if the graph
opens down, its height is maximum at the vertex.

If a quadratic is given in the form 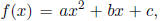then the x-coordinate of its
vertex is 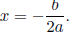Since you already know the quadratic formula, you can remember it as
part of the formula:



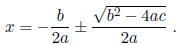
This way of looking at the quadratic formula shows that if the graph has x-intercepts, they
occur as points on either side of the line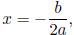 which is the axis of symmetry of the
graph. The summary on page 301 explains the steps in graphing a quadratic function.

Review problems: p302 #13,15,27,31,37,43,55,61,81,83

4.1 #29. Solve f(x) ≤g(x) for f(x) = 4x - 1 and g(x) = -2x + 5

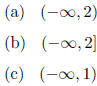
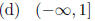
(e) None of these

4.1 #37c. The cost (in dollars) of renting a truck is C(x) = 0.25x+35, where x is the number
of miles driven. If you want the cost to be no more than $100, what is the maximum number
of miles you can drive?

(a) 60
(b) 260
(c) 400
(d) 540
(e) None of these

4.3 A. If f(x) is a quadratic function whose graph has the vertex (h, k), which one is the
correct form of the function?

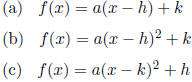
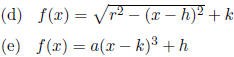
4.3 #42 If f(x) = x² - 2x - 3, then the vertex of the graph of f(x) is

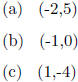
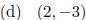
(e) None of these

4.3 B. Find the vertex of the quadratic function f(x) = 2x² - 4x + 9.

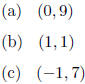
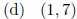
(e) None of these
 

4.3 C. Find the axis of symmetry of the graph of f(x) = 4x² - 8x + 3.

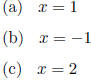
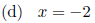
(e) None of these

4.3 D. Let f(x) = 4x² - 8x + 3. Find the x and y-intercepts, if any.

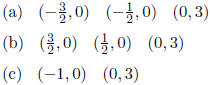
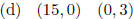
(e) None of these

4.3 #55. Find the equation of the quadratic function whose graph has vertex (-3, 5) and
y-intercept -4.

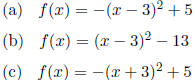
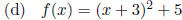
(e) None of these

4.3 #61. Find the minimum value of the function f(x) = 2x² + 12x - 3.

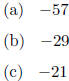
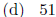
(e) None of these

4.3 #62. Find the minimum value of the quadratic function f(x) = 4x² - 8x + 3.

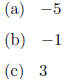
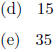
4.3 #81. Suppose that the manufacturer of a gas clothes dryer has found that when the
unit price is p dollars the revenue R (in dollars) is R(p) = -4p²+4000p. What is the largest
possible revenue? That is, find the maximum value of the revenue function.

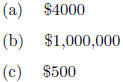
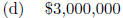
(e) None of these

4.3 E. A store selling calculators has found that, when the calculators are sold at a price
of p dollars per unit, the revenue R (in dollars) as a function of the price p is R(p) =
-750p² + 15000p. What is the largest possible revenue? That is, find the maximum value
of the revenue function.

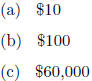
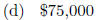
(e) None of these

Answer Key

4.1 #29. (d)
4.1 #37c. (b)
4.3 A. (b)
4.3 #42 (c)
4.3 B. (d)
4.3 C. (a)
4.3 D. (b)
4.3 #55. (c)
4.3 #61. (c)
4.3 #62. (b)
4.3 #81. (b)
4.3 E. (d)

Solutions

4.3 A. If f(x) is a quadratic function whose graph has the vertex (h, k), which one is the
correct form of the function?
Solution: (b) f(x) = a(x - h)² + k

4.3 B. Find the vertex of the quadratic function f(x) = 2x² - 4x + 9.
Solution: (d) The text gives this formula: the x-coordinate of the vertex of the graph
of f(x) = ax² +bx+c is 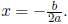In this example, a = 2 and b = -4, so the vertex occurs
at 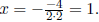 Then f(1) = 2 - 4 + 9 = 7 gives the y-coordinate.

If you forget the formula, you can always complete the square:

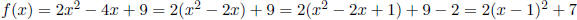
so h = 1 and k = 7 and the vertex is (1, 7).

4.3 C. Find the axis of symmetry of the graph of f(x) = 4x² - 8x + 3.
Solution: (a) The axis of symmetry passes through the vertex, which has x-coordinate
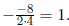The axis of symmetry is the line x = 1.
Again, if you forget the formula, complete the square:

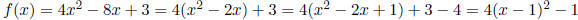
This shows that the vertex is at (1,-1).

4.3 D. Let f(x) = 4x² - 8x + 3. Find the x and y-intercepts, if any.
Solution: (b) Since f(0) = 3, the y-intercept is (0, 3).
To find the x-intercept, solve 4x² - 8x + 3 = 0. This can be factored as
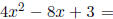
(2x - 1)(2x - 3), so 2x - 1 = 0 or 2x - 3 = 0, giving the x-intercepts 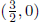and

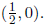
4.3 #62. Find the minimum value of the quadratic function f(x) = 4x² - 8x + 3.
Solution: (b) The minimum value occurs at the vertex, which has x-coordinate
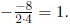
Then f(1) = -1 is the minimum height.

4.3 E. A store selling calculators has found that, when the calculators are sold at a price
of p dollars per unit, the revenue R (in dollars) as a function of the price p is R(p) =
-750p² + 15000p. What is the largest possible revenue? That is, find the maximum value
of the revenue function.

Solution: (d) The graph is a parabola, opening down, so to find the maximum value we
need to find the y-coordinate of the vertex. We get
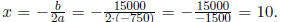
The maximum revenue is R(10) = -750(10)² + 15000(10) = -75000 + 150000 = 75000.