A Joyful Introduction to Matrices

Outline

Basics
Overview

Addition and multiplication
matrix addition
matrix multiplication
Special types of matrices

Inverse

Summary

Definition

A matrix is an array of elements.
Each element is the data on one variable for one case.
For example, consider the following table of data (and then we
will look at the matrix version)

Table 1

wage	gender	occupation
15	0	1
17	0	1
18	0	0
16	1	1
20	1	0
21	1	0

Example

we can present this information from Table 1 in matrix 1

15	0	1
17	0	1
18	0	0
16	1	1
20	1	0
21	1	0

Matrix 1 has 6 rows and 3 columns (a 6 × 3 matrix)
Each row of the matrix represents the data for one person
Each column is the data on one variable

Why use them?

Matrix notation is a much easier way to explain multiple
regression
1-variable :
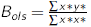
where
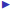multiple variables: 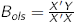where x and y are matrices, and
x' is the transpose of x (we'll talk about that in a moment)

Y vector

I A matrix with one row or one column is a vector.
If wages are going to be are dependent variable, we can
represent them in vector format:

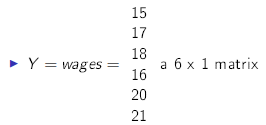
X matrix

Likewise, we can represent our independent (explanatory)
variables in the x matrix:

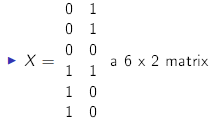
the first column is gender
the second column is occupation

transpose

The transpose of a matrx m is a matrix m' where the element
x_ij of m becomes x_ji
i.e. switch the rows and columns
Example:

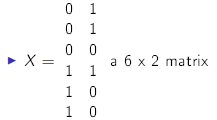
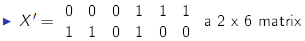
matrix addition
matrix multiplication
Special types of matrices

Matrix Additon

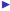You can add two matrices with the same dimensions together
by adding the elements ij together
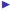Example

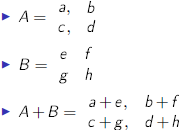
matrix multiplication by a scalar

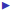Example

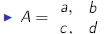
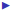if z is a scalar (i.e., not a matrix), then

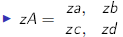
multiplication by a matrix . . . dimensions

multiplying two matrices together is more complicated
we can multiply two matrices A (a r × c matrix) and B (a c × q
matrix)
the number of columns of A must equal the # of rows of B
If the elements of A are a_ij and the elements of B are b_ij then
AB=C
where the elements of C,

Example

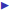Example

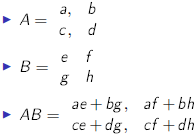
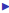visually, for the ijth element, take the ith row of A, rotate it 90
degrees, and align it with the jth column, multiply the
elements and add the results.

In class question

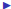Now you do it.

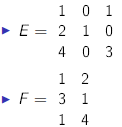
What is F'E (the transpose of F times E)? What are the
dimensions of the resulting matrix?
Another question. If A is a 5 × 1 matrix, what dimensions will
A'A have? What about AA'?

Symmetric

A symmetric matrix is a square matrix where A'=A.
Question: Write down a symmetric matrix

Diagonal

A diagonal matrix is one whose o -diagonal elements are all 0.
Example: (put on board)

Identity

an identity matrix is a diagonal matrix with ones down the
diagonal.

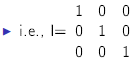
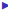It is called an identity matrix because IA=A=AI

Scalar

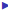A scalar matrix is a diagonal matrix where the diagonal
elements are all the same.

Variance-covariance matrix (p.202)

(Reference: p.202 NWK)
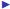The variance-covariance matrix is the matrix of variances
(along the diagonal) and covariances of the random variables
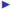Example. We have three random variables A, B, C (put on
board)

inverse

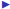For scalars, it is easy to calculate the inverse. The inverse of 3
is 1/3.
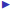3*1/3=1
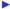I The inverse matrix is the matrix A^-1such that AA^-1 = I , the
identity matrix.
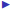It is easy to calculate the inverse of a diagonal matrix.

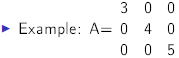
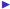Inverse = (put on board)

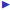For nondiagonal matrices it is more difficult to calculate the
inverse (but it can be done, provided the inverse exists).
For our purposes, it is sufficient that you recognize what I
mean when I refer to an inverse matrix.

Summary

Matrix notation is a concise way to represent cases with multiple
variables.
Each row represents a case.
Each column represents a variable.
real world data is in matrix form (i.e., a big table)
We will use matrix notation in our discussion of multivariate
regression, which is where things get more interesting.
We have learned basic matrix operations: addition, multiplication,
transpose, and inverse