Torticelli's Law

One afternoon, I filled a 25-gallon cooler about half-full with water, put a yardstick in it, and
opened the stop-cock to let the water out. I took measurements periodically as the cooler
emptied. The data I gathered is in Table 1 below. The cooler was cylindrical in shape with a
radius of 10 inches.

Table 1: Time and Depth of water in an urn

Torticelli’s Law says that, under these conditions, the change in volume (V) should be
proportional to the square root of the depth (h) of fluid. So, 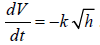. We also know that
V =π r²h .

Solution:
a) Solve the differential equation to find h as a function of t. What type of function is h(t )?
We know that 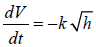and that V =π r²h , so 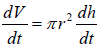since r is a constant 10 inches.
We have the differential equation 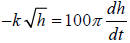. We can simplify the notation by letting
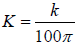and solve by separating variables.

So, 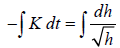implies that 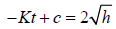and 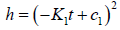for t ≥ 0 . This is a
quadratic equation. In this last equation,.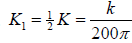

b) Fit a model of this type to the data in Table 1.

To find a quadratic of the form 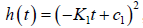, we can graph the ordered pair
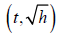
If 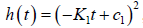, then the graph of 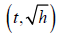should be a line with a slope of  K₁ and an
intercept of c₁ . Re-expressing the data this way does give us a linear model (see graph below)
with a regression equation of Y₁ = −0.005x + 3.53, or, more correctly, 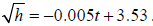This
means that h = (−0.005t + 3.53)² should fit the original data well.

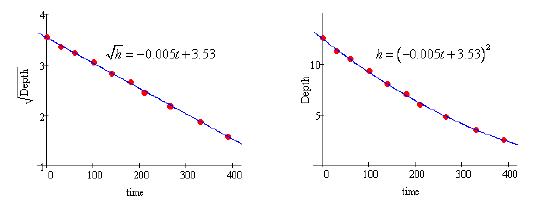
As the graphs show, the models are quite good. We also see that K₁ ≈ 0.005 and c₁ ≈ 3.53 .

You could also use your calculator to fit a quadratic model, then factor to find K and c. Reexpression
in linear form is a better approach, since we know that a quadratic function can be a
good approximation to any continuous function over some small interval in its domain.

c) After how many seconds is the depth decreasing at a rate of 0.025 inches/sec?
If 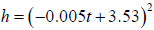, then dh/dt =  2( -0.005t 3.53)( -0.005) = 0.00005t - 0.0353.
So, the depth is dropping at 0.0353 inches/second initially (when the depth is 12.5 inches) and
0.0203 inches/second after five minutes (when the depth is 4.12 inches) and 0.0053
inches/second after 10 minutes, when it is almost empty (about a fourth of an inch).
To find the time at which the depth decreasing at a rate of 0.025 inches/sec, we set dh/dt =  -0.025
and solve 0.00005t − 0.0353 = −0.025 . So, t = 206. After approximately 206 seconds, the water
level is dropping at a rate of .025 inches/second.

d) Suppose after 2 minutes water is added at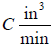 . What value of C would keep the depth
of the water constant?

Since 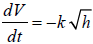. From a) we know that 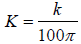and K₁ = 1/2K . From b) we saw that

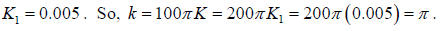
So, 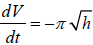. After 2 minutes, the depth is h = (−0.005 (120) + 3.53)² = 8.58 inches, so
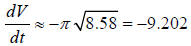cubic inches per second or, equivalently, 552.12 cubic inches per
minute.

Super Challenge: (0 points, just for fun, no calculus necessary)
e) When the cooler is full, the center of mass of the cooler with water is about in the center
of the cooler (a little lower than the center since the top is not on the cooler). As the water flows
out, the center of mass of the cooler-with-water drops, decreasing continuously. But, when the
tank is empty, the center of mass is magically again in about the center of the cooler. So, at
some point, while the water level is dropping, the center of mass began to rise. Describe the
conditions at which the center of mass reaches its lowest level.

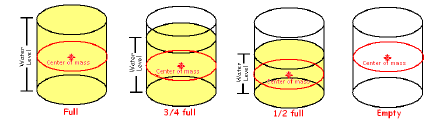
The lowest the center of mass will be is when the water level and the center of mass coincide. A thought
experiment will illustrate why this is true. It is easier to see if you think about the water being a solid
(frozen, if you like) so you can set the cooler on a balance.

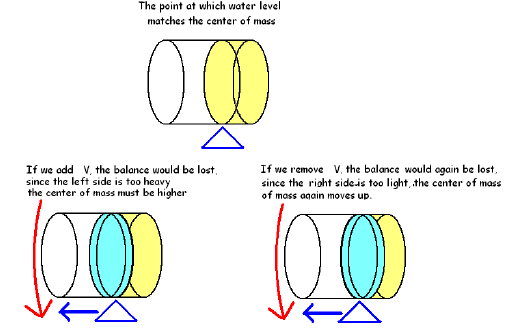
By the Intermediate Value Theorem, there is a point at which the center of mass coincides with the water
level (you can’t go continuously from below the water level to above the water level without passing
through the water level). This point is where the center of mass is the lowest.
Consider the point at which the cooler balances at the water level.

A few seconds earlier, there was more water in the tank. If the fulcrum stays at the same point, the cooler
would be unbalanced, since its left side (top) is too heavy. The center of mass must move left (up) to
accommodate this.

A few seconds later, there will be less water in the tank. If the fulcrum stays at the same point, the cooler
would again be unbalanced, since its right side (bottom) is too light. The center of mass must again move
left (up) to accommodate this.

Thus, the center of mass will be at its lowest at this point.