Try the Free Math Solver or Scroll down to Tutorials!
 

 

 

 

 

 

 

 
 
 
 
 
 
 
 
 

 

 

 
 
 
 
 
 
 
 
 

Please use this form if you would like
to have this math solver on your website,
free of charge.

Quadratic Equations and Functions

Graphing Functions

Problem I: For the function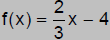
Set the Window on your calculator as given:
Xmin = -1
Xmax = 1
Xscl = 0.5
Ymin = -1
Ymax = 1
Yscl = 0.5

Graph the function.
a. What graph do you see?
b. Why do you think this is happening?

Set the Window on your calculator as given :
Xmin = -5
Xmax = 5
Xscl = 1
Ymin = -5
Ymax = 5
Yscl = 1

Graph the function.
c. What graph do you see?
d. Is this what you would expect the graph
to look like?
e. Can you see all of the intercepts?

Set the Window on your calculator as given:
Xmin = -4
Xmax = 10
Xscl = 1
Ymin = -6
Ymax = 5
Yscl = 1

Graph the function.
f. What is the name of this kind of function?
Why?
g. What are the intercepts?

 Problem 2: For the function f(x) = 9x - 0.1x2

Set the Window on your calculator as given
Xmin = -10
Xmax = 10
Xscl = 1
Ymin = -10
Ymax = 10
Yscl = 1

Graph the function.
a. What graph do you see?
b. Is this what you would expect the graph to
look like?

Set the Window on your calculator as given:
Xmin = -25
Xmax = 100
Xscl = 10
Ymin = -50
Ymax = 50
Yscl = 5

Graph the function.
c. What graph do you see?
d. Do you think you are seeing all important
characteristics of the graph?

Set the Window on your calculator as given:
Xmin = -50
Xmax = 100
Xscl = 10
Ymin = -50
Ymax = 250
Yscl = 20

Graph the function.
e. What graph do you see?
f. Do you think all important characteristics of
the graph are visible?
g. How do you know? Explain your answer.
Problem 3: For the function
f(x) = 0.1x3 - 1.5x2 + 8

Set the Window on your calculator as given:
Xmin = -10
Xmax = 10
Xscl = 1
Ymin = -10
Ymax = 10
Yscl = 1

Graph the function.
a. What graph do you see?
b. Is this what you would expect the graph
to look like?

Set the Window on your calculator as given:
Xmin = -20
Xmax = 20
Xscl = 5
Ymin = -20
Ymax = 20
Yscl = 5

Graph the function.
c. Are all the turning points visible?
d. How many turning points do you expect
there to be?

Set the Window on your calculator as given:
Xmin = -5
Xmax = 20
Xscl = 5
Ymin = -50
Ymax = 20
Yscl = 5

Graph the function.
e. Is this what you would expect the graph
to look like?
f. How can you decide that this window
shows all important characteristics of the
graph?

 Problem 4: For the function
f(x) = x4 - 8x2 - 10

Set the Window on your calculator as given:
Xmin = 1.5
Xmax = 4
Xscl = 1
Ymin = -35
Ymax = 10
Yscl = 1

Graph the function.
a. What shape does the graph appear to have?
b. Is this what you would expect the graph
to look like? Why?

Set the Window on your calculator as given:
Xmin = -1
Xmax = 4
Xscl = 1
Ymin = -35
Ymax = 25
Yscl = 5

Graph the function.
c. Do you think you are seeing all important
characteristics of the graph?
d. Are all of the intercepts visible?

Set the Window on your calculator as given:
Xmin = -5
Xmax = 5
Xscl = 1
Ymin = -35
Ymax = 10
Yscl = 5

Graph the function.
e. Do you think you are seeing all important
characteristics of the graph?
f. How do you know? Explain your answer.
Problem 5. For the function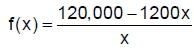
Set the Window on your calculator as given:
Xmin = -10
Xmax = 10
Xscl = 1
Ymin = -10
Ymax = 10
Yscl = 1

Graph the function.
a. What graph do you see?
b. Why do you think this is happening?

Set the Window on your calculator as given:
Xmin = 0
Xmax = 140
Xscl = 10
Ymin = -100
Ymax = 100
Yscl = 10

Graph the function.
c. What graph do you see?
d. Is this what you would expect the graph
to look like?

Set the Window on your calculator as given:
Xmin = 0
Xmax = 200
Xscl = 50
Ymin = -2000
Ymax = 5000
Yscl = 1000

Graph the function.
e. Are all important characteristics of the
graph visible?
f. Do you expect there to be more
intercepts?

 Set the Window on your calculator as given:
Xmin = -200
Xmax = 200
Xscl = 50
Ymin = -2000
Ymax = 5000
Yscl = 1000

Graph the function.
g. Are all important characteristics of the
graph visible?
h. What part of the Window do you think
needs to be adjusted?

Set the Window on your calculator as given:
Xmin = -200
Xmax = 200
Xscl = 50
Ymin = -6000
Ymax = 5000
Yscl = 1000

Graph the function.
i. Are all important characteristics of the graph
visible?
j. How do you know? Explain your answer.

Rational Functions

1. For each of the following rational functions:
a. Find the domain.
b. Find the vertical asymptote(s), if any. If no vertical asymptote, write “No VA”.
c. State whether the function has a horizontal asymptote, a slant asymptote or
neither; then state the equation of the horizontal or slant asymptote, if any.

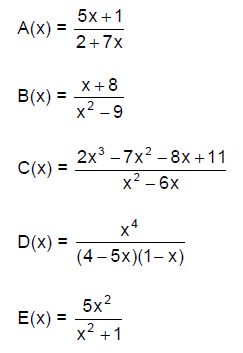
2. A rare species of insect was discovered in the rain forest. In order to protect the species,
environmentalists declare the insect endangered and transplant the insects into a
protected area. The population of the insect t months after being transplanted is
given by P(t).

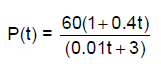
a. How many insects were discovered? In other words, what was the population
when t = 0?
b. What will the population be after 5 years?
c. Determine the horizontal asymptote of P(t). What is the largest population that the
protected area can sustain?
d. Graph P(t).

Polynomial and Rational Inequalities

Solve the following polynomial inequalities by first writing them in general form, factoring (if needed) to identify boundary points, drawing a number line with boundary points labeled, and testing each interval. Express the solution in interval notation.
1. x2 > 7x
2. 12x2 < 37x + 10
3. (x + 2)(x – 5)(x + 7) ≤ 0

Solve the following rational inequalities by first writing them as a single simplified rational expression on one side and zero on the other side of the inequalities. Identify the boundary points by labeling them on a number line and then testing the intervals. Express the solution in interval notation.

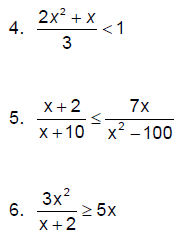
Applications
7. The profit from selling x pieces of handmade jewelry can be modeled by the
equation P(x) = –x2 + 130x – 3000. What is the range of profitable orders (P(x) > 0)?

8. The difference between the value of a piece of equipment and what is owed on it is
modeled by the expression 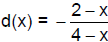, where x is the number of years since
the equipment was purchased. When does the amount owed exceed the value of
the equipment (d(x) < 0)?