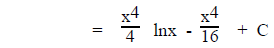INTEGRATION MATH 21 B

5. Algebraic Substitution. Let u = the part that is keeping it from being an exponent
problem. [See I. A.]

This method is last in the list because it is not always clear what to let u equal. Some people find this method
easy and use it instead of long division. The problem used as an example for long division may be done using
this method by letting u = x + 1.

Recall that expressions in parentheses raised to a fractional or negative power cannot be written as an exponent
problem. In this case it is often useful to let u = the part inside the parentheses , solve for x and dx and then
substitute.

For example: 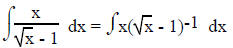Note the exponent outside the parentheses

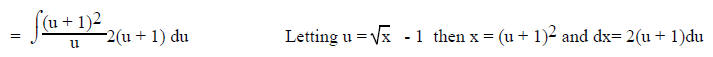
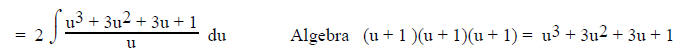
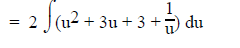
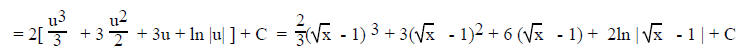
II. Trig
A. Does the derivative of one part = the other part?

A word hear about memorization. It is critical that you know your derivatives of the trig functions extremely
well. If not, you will have trouble recognizing that "the derivative of one part = the other part."

1. If one trig term, let u = the angle.
For example: 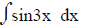Letting u = 3x, du = 3dx One trig term & the angle is 3x

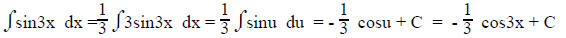
2. If more than one trig term, let u = one of the trig terms

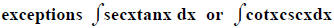
For example: Note that if u = tanx , du = sec²x dx so

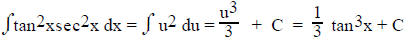
B. Tricks

1. If powers of sines and/or cosines
a. If the power of sine or cosine is odd - take one from the sine or cosine which is
raised to an odd power, use the identity sin²x + cos²x = 1 to rewrite the part that
was changed and let u = the one you didn't change.

For example: 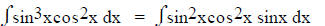Taking sinx from the one w/ the odd power

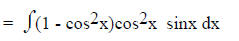Using the identity to change sin2x
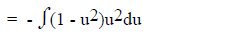letting u = cosx, du = -sinxdx

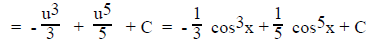
b. If sine and/or cosine to even powers
use 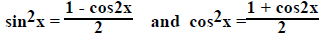until there are no even
powers of sine or cosine left.

For example:
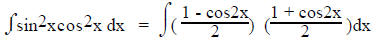  Using the identities
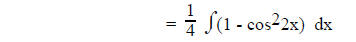Algebra
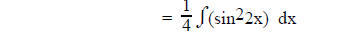Identity
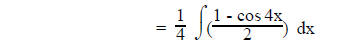Identity

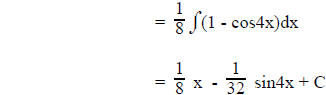
2. If sines and cosines with different angles. Use the appropriate identity
sinA cosB =1/2 sin(A + B) + 1/2 sin(A - B),
sinA sinB = 1/2 cos(A - B) - 1/2 cos(A + B) or
cosA cosB = 1/2 cos(A - B) + 1/2 cos(A + B)

For example:
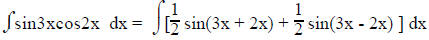  Using the identity

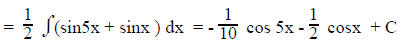
3. If rational expression involving sine and/or cosine, let 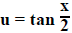then

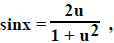
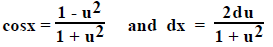
For example:

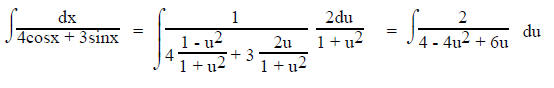
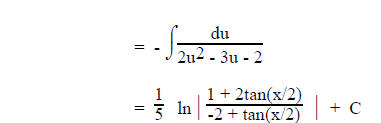Using partial fractions (See I.C.2.)

4. If powers of tangent and/or secant
a If the secant is to an even power - take sec²x from the secant term, change
remaining secant term to tangent using sec²x = tan²x + 1, let u = tanx

For example:

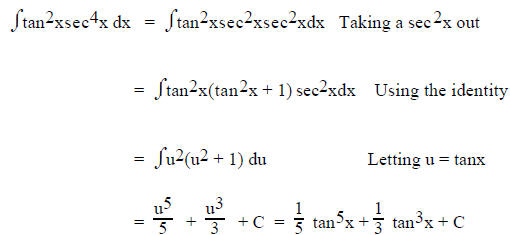
b. If tangent is to an odd power - take a secant and a tangent from the integrand,
change the remaining tangent term to secant using tan²x = sec²x - 1 and let u = secx.

For example:

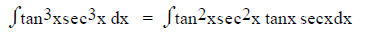Factoring out tanx and secx
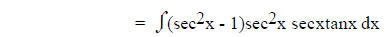Identity
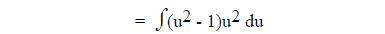u = secx

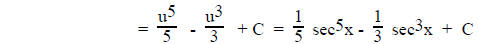
III. Mixture (some combination of algebra, trig, inverse trig, logs and/or exponentials)
A. Does the derivative of one part = the other part?

Read the explanations in I. B. and II. A. again. It is also critical to know the derivatives of 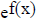,ln f(x) and of
the inverse trig functions.

For example: 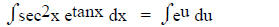Letting u = tanx

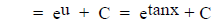
B. Integration by parts - LIATE

The letters in the acronym stand for Logarithms, Inverse trig, Algebra, Trig and Exponentials (e^x not x³). It
usually works to let u = the part that comes first in the word, LIATE.

Recall that

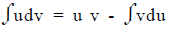
For example: 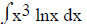is composed of an Algebra part (x³) and a Log part (lnx). So let u = lnx (L comes

before A in LIATE). So u = lnx dv = x³dx (the rest of the integrand) then 

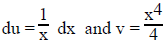
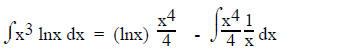Using the Int. by Parts Formula
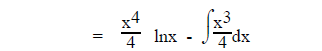Algebra