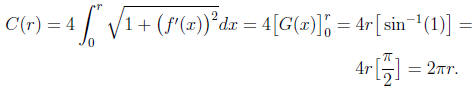THE AREA AND CIRCUMFERENCE OF A CIRCLE
Proofs
So much for history. The rest of this article is devoted to
giving some simple, elementary proofs of Ideas 1 through 5
above.
Ideas 1 and 2. I claim that Ideas 1 and 2 are actually quite
obvious, once you think about them for a moment. (I do not
claim this about Idea 3 though.) I will give an informal proof
of Ideas 1 and 2. My informal proof can be turned into a formal
proof in a number of different ways. Let us x some circle Ω.
Let C be the circumference of Ω, A the area of Ω, and r the
radius of Ω. Let k = C/r and let h = A/r2. Now let Ω' be
any other circle, let A' be its area, C' its circumference, and
r' its radius. We want to see that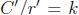 
and
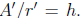
But I claim that this is obvious, because Ω' can be obtained
by simply expanding or contracting Ω.
Let me be a bit more rigorous. Let us introduce a coordinate
system to aid in the discussion. The coordinate system is not
essential to my proof, but it will simplify the discussion. In
order to exhibit how elementary and intuitive my proof is, I
will make as little use of analytic geometry as possible. Since
both area and arc length are intuitively preserved by "rigid
motions," we may as well assume that both of our circles are
centered at the origin. Also, to be concrete, let us assume that
Ω' is a bigger circle than Ω, i.e. that r' > r. Let α= r'/r. By
the term "circle" we mean the set of all points a given distance
from a center point. Thus Ω is the set of all points located a
distance r' from the origin, and Ω' is the set of all points located
a distance r' from the origin. Consider the transformation
T of the coordinate plane which sends a point (x, y) to the
point (α x, αy). T is an "expansion" by a factor of α. Suppose
that (x, y) is a point on the circle Ω. Then the distance from
(x, y) to the origin is r. T sends the point (x, y) to the point
( αx, αy). Using some simple facts about similar triangles, we
see that the distance from ( αx, αy) to the origin is αr = r'.
Thus ( αx, αy) lies on the circle Ω'. Thus the transformation
T maps Ω onto Ω'. Let us see what T does to area and arc
length. Again using some simple facts about similar triangles,
it is easy to see that if 
and
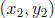are any two points
in the plane and the distance between them is d, then the
distance between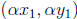 
and
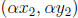is αd. That is,
T increases all distances by a factor of α. It follows that T
increases the length of any polygonal path by a factor of α.
Since our intuitive notion of arc length corresponds to the limit
of the lengths of approximating polygonal paths, it follows that
T increasing all arc lengths by a factor of α. As T sends Ω onto
Ω' it follows that C' = αC. Thus
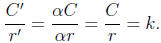
Also, since T increases all distances by a factor of α, T
increases
the area of any square by a factor of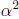 
. Since
our
intuitive notion of area corresponds to the limit of the areas of
approximating collections of squares, T increases all areas by
a factor of 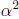. As T sends Ω onto Ω' it follows
that
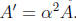
Thus
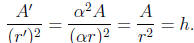
In summary, Ideas 1 and 2 follow immediately from the fact
that expansions and contractions act linearly on the distance
between two points. The fact that this is so is an integral part
of our geometric intuition. It is the reason why two similar
triangles have the same ratios of side lengths.
Idea 3. Unlike Ideas 1 and 2, I do not claim that
Idea 3 is
obvious. The proof of Idea 3 requires a more detailed analysis.
Below I will give some arguments which will reprove Ideas 1
and 2, and also yield a proof of Idea 3.
My goal is to derive Ideas 1, 2, and 3 using "geometrically
intuitive" reasoning. At several points I will even appeal to
a diagram to make my argument. It is well known that such
appeals to diagrams are dangerous, as diagrams can often be
misleading. To give a completely rigorous geometric proof, I
would have to give a list of geometric axioms, and derive all of
my results from these axioms. I will not do this here, because I
would like to keep this article short and simple. The interested
reader is invited to try to translate my proof into a completely
rigorous proof based on a set of axioms.
Definition 1. Let A(r) = the area of the circle of radius r.
To understand my proof, pretend again that you have never
heard of the number π. Now I will define π for you.
Definition 2. Let π= A(1).
In the proof below I will mention the trigonometric functions
sin, cos and tan. Since I intend to use only "geometrically
intuitive" reasoning, I would like to point out that these
trigonometric functions can be defined on acute angles, with no
other assumptions besides the fact that similar triangles have
the same ratio of side-lengths.
For convenience, I will use radians to measure angles. In
so doing, I must be careful to avoid "begging the question."
When we first encounter radians in a mathematics class there
are two important facts we learn. (i) There are 2π radians of
angle measure in a full circle, and (ii) An angle of one radian
inscribed in a circle of radius r cuts o a circular arc of length r.
From these two properties of radian measure we could conclude
immediately that the circumference of a circle is given by C =
2πr. This of course would be a "circular argument." That is
to say, it would be cheating. The reason is the following. Fact
(ii) is usually taken as the definition of radian measure. Then,
the formula C = 2π r is used to see that fact (i) is true. So
it would be cheating to use facts (i) and (ii) in order to prove
that C = 2π r. To avoid this problem I will not assume fact
(ii) above. Instead I will define radian measure so that fact (i)
above holds. That is, let us define one radian to be the same
angle measure as [360÷ (2π )]° . Later, when we have proven
the formulas A = πr2 and C = 2π r, then fact (ii) above will
follow.
Lemma 3. For any real number r > 0 and any real number θ
with 0 < θ< π/2, we have the following.
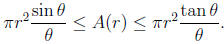
Proof. Consider the following diagram, in which o is the
center
of the circle, and 
oac is a right angle.
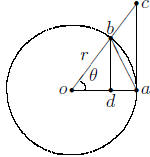
Notice that the area of the triangle oab
is less than the area of the circular segment oab which is less
than the area of the triangle oac. 
the area
of
triangle oab is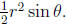 
The area of the
circular segment oab
is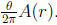 
The area of triangle oac is
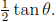Thus we have.
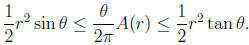
Multiplying through by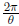 
we have
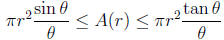
which is what we were trying to prove.
From the above lemma we can immediately derive a famous
limit theorem.
Corollary 4. If θ is measured in radians, then
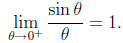
Proof. Recall that we have defined π= A(1). Setting r = 1
in
the previous lemma we get.
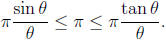
Canceling the term π we get
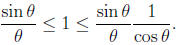
Multiplying through by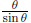 
yields
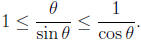
Inverting the fractions and reversing the inequalities yields.
Just by thinking about right triangles, it is easy to see
that as
θ gets closer and closer to 0, cosθ gets closer and closer to the
value 1. In symbols we write this as
From formulas 1 and 2 it follows that
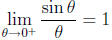
which is what we were trying to prove.
From the previous two results we can derive the formula for
the area of a circle.
Theorem 5. For all r > 0, A(r) = πr2.
Proof. By taking the limit as θ goes to 0 in Lemma 3 and then
applying Corollary 4 we get.
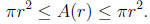
Now we turn to the circumference of a circle.
Definition 6. Let C(r) = the circumference of the circle of
radius r.
The next theorem will complete the proof of Ideas 1, 2, and
3.
Theorem 7. For all r > 0, C(r) = 2πr.
Proof. The circumference of a circle is equal to the limit as n
goes to infinity of the perimeter of an inscribed regular n-gon.
Let us calculate this perimeter. The following figure illustrates
the situation in the case n = 6.
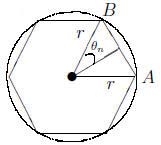
Let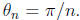 
In the figure, we
have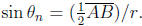 
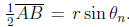So
So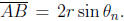 
So
the perimeter of an
inscribed regular n-gon is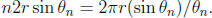 
So
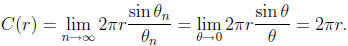
Ideas 4 and 5. Finally, we will discuss one
elementary way
to calculate approximations to the number π. In Lemma 3
above, let r = 1 and let θ= π/n. The result is the following
inequality.
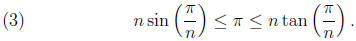
If we let n = 6 we get
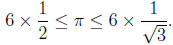
If we then use the approximation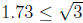 
,
we arrive at the
rough approximation
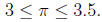
This approximation is rough, but at least we have proved
it,
and using very elementary techniques.
The inequalities in 3 can in principle be used to estimate
π with as much accuracy as we desire. If we make the integer
n larger and larger, we will get more and more accurate
estimates. Of course this still leaves us with the problem of estimating
sin( π/n) and tan( π/n). Notice that the solution "use
a calculator to estimate sin( π/n) and tan( π/n)" is of no help at
all. We could of course use our calculator to immediately find
an estimation of π to 8 decimal places. But then we wouldn't
understand how the calculator is arriving at this estimate. The
whole point is to prove our estimate of π using elementary techniques.
The half-angle formulas from trigonometry will come
to our rescue.
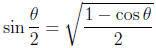and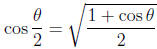 
Since we know sin( π/6) and cos( π/6), using the
half-angle formulas
repeatedly will allow us to calculate sin( π/n), cos( π/n),
and tan( π/n), for n = 6, 12, 24, 48, 96, . With n = 12 we
get the estimate
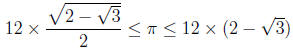
and by approximating the square roots we get
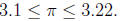
With n = 24 we get the estimate
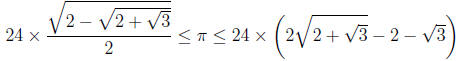
and by approximating the square roots we get
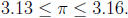
As you can see, our method of approximating π is not very
efficient. There are far more efficient algorithms for estimating
π, but we will not go into them here.
A Different Point of View
In the previous section I took the point of view that it is
desirable to prove the formulas A = πr2 and C = 2 πr using
geometrically intuitive reasoning, and using as little abstract
analysis as possible. It is also possible to take the opposite
point of view, namely that it is desirable to prove the two
formulas using no geometric reasoning, and using only abstract
analysis. I conclude this article with a quick sketch of how one
might do this.
To begin with, one can define the circle of radius r to be
the graph of the p equation x2 + y2 = r2. Then,
letting f(x) =
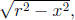one can define the area and circumference of
this
circle with the formulas
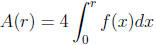and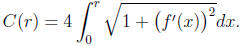 
Then one can define the sine and cosine functions by the
familiar
power series.
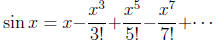and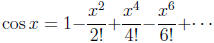 
With these definitions alone, and without appealing to geometry
at all, one can prove all of the familiar properties of the
trigonometric functions. In particular one can prove that for
all x, sin2 x + cos2 x=1, that sin
and cos are periodic functions,
and that the derivative of the function sin x is cos x, and
the derivative of the function cos x is −sin x. Then one can
define the number π as half the period of the sin function.
Then one can prove that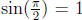 
, that
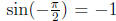and
that sin x is a one-to-one function on the interval [− π/2, π/2].
Now let sin−1 x be the inverse of the function sin x over the
interval [− π/2, π/2]. So sin−1(1) =π/2, and sin−1(0) = 0.
Letting
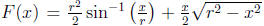and letting G(x) =
r sin−1(x/r) one can prove that
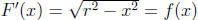and
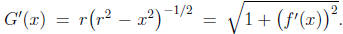Finally, one can
conclude that
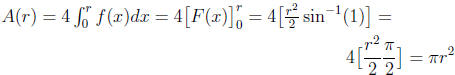
and that
