Solving Systems of Linear Equations by Elimination
1. The elimination method for solving linear
systems is based on the addition
property of equality. Add equal quantities (rather than the same quantity)
to
both sides of an equation to eliminate a variable.
If A= B and C=D, then A+ C=B+ D
2. This method is easier to use than the substitution method if none of the
variables
in the system have a coefficient of 1 or -1.
3. Key Idea: Make the coefficients of one variable in each equation the
same in
absolute value but with different signs. Then adding the two equations will
eliminate this variable.
4. Elimination Method: (See page 568.)
Step 1: Write both sides of each equation in the form
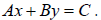
Step 2: Multiply one or both of the equations by non-zero numbers that
will
make the coefficients of one variable in each equation the same except for sign.
(The coefficients of one variable must be opposites.) Be sure to multiply each
term of both sides of an equation by the required number. (The goal is to obtain
a
zero coefficient for one variable after the equations are added.)
Step 3: Add the new equations to eliminate a variable. The sum will be an
equation in one variable.
Step 4: Solve the equation in one variable that you obtained in step 3.
Step 5: Substitute the solution obtained in step 4 into either original
equation and
solve for the other variable.
Step 6: Check the solution in both of the original equations.
Step 7: State the solution set. If the solution is a single point, give
the answer as
an ordered pair with x value in the first position and y value in the second
position. (Remember that you are not done until you have values for both x and
y.)
5. It does not matter which variable you eliminate first.
6. To find the second variable it is sometimes easier to repeat the
elimination
procedure instead of substituting in a value. This is often the case if the
first
solution is a fraction.
7. As in the last section, the system has no solutions
if the equation in found in Step
3 is a statement that is false. The system will have infinitely many
solutions if
the statement found in Step 3 is always true.
8. Choosing a method to solve a system of linear equations. (Note that
either
method can always be used. But, one is often easier than the other. See page
574,)
a. If one of the equations is already solved for one variable, try substitution.
b. If both equations are in the form
and none of the
variables
have a coefficient of 1 or -1, use elimination.
c. If both equation are in the form
and one of the
coefficients
is 1 or -1, then use either method.
