MATH 360 Review of Set Theory
5. Theorem: Suppose A, B and C are sets. Prove that
A∪ (B ∩ C) = (A ∪B) ∩
(A ∪ C).
Proof: We need the definitions of set equality and of subsets. We need to
prove
two things:
A ∪ (B ∩ C) 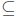 (A ∪ B) ∩
(A ∪ C)
(A ∪ B) ∩
(A ∪ C)
A ∪ (B ∩ C) 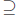 (A ∪ B) ∩ (A ∪ C)
(A ∪ B) ∩ (A ∪ C)
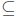 : Let x ∈ A ∪ (B ∩ C).
Then x ∈ A or x ∈ B ∩ C.
: Let x ∈ A ∪ (B ∩ C).
Then x ∈ A or x ∈ B ∩ C.
• If x ∈ A, then x ∈ A ∪ B and x ∈ A ∪ C by definition of union. Thus
x ∈ (A ∪ B) ∩ (A ∪ C) by definition of intersection.
• If x ∈ B ∩ C, then x ∈ B and x ∈ C. Thus x ∈ A ∪ B and x ∈ A ∪ C by
definition of union. Thus x ∈ (A∪B)∩(A∪C) by definition of intersection.
Either way, x ∈ (A ∪ B) ∩ (A ∪ C). Thus we have proved A ∪ (B ∩ C) 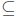
(A ∪ B) ∩ (A ∪ C)
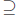 : Let x ∈ (A ∪ B) ∩ (A ∪ C). Then x ∈ A ∪ B
and x ∈ A ∪ C. Now there are
: Let x ∈ (A ∪ B) ∩ (A ∪ C). Then x ∈ A ∪ B
and x ∈ A ∪ C. Now there are
two choices: either x ∈ A or x 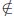 A.
A.
• If x ∈ A, then x ∈ A ∪ (B ∩ C) by definition of union.
• If x 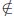 A, then x ∈ B and x ∈ C by definition
of unions. Thus x ∈ B ∩ C
A, then x ∈ B and x ∈ C by definition
of unions. Thus x ∈ B ∩ C
by definition of intersections. Thus x ∈ A ∪ (B ∩ C).
Either way, x ∈ A∪(B∩C). Thus we have proved A∪(B∩C) 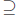 (A∪B)∩(A∪C),
(A∪B)∩(A∪C),
which, together with the first part, proves A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
6. Theorem: DeMorgan's Laws: X − (A ∪ B) = (X − A) ∩ (X − B)
Proof: Again, we need two parts to the proof: 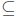 and
and 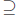 .
.
Let x ∈ X − (A ∪ B). 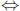
x ∈ X but x 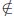 A ∪ B
A ∪ B 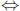
x ∈ X but x 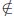 A and x
A and x 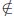 B
B 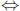
x ∈ X − A and x ∈ X − B 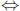
x ∈ (X − A) ∩ (X − B).
Note: This time, rather than being forced to prove this in two separate parts
like the previous proof (i.e. first proving 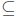 then
then 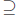 ) we were able to combine
) we were able to combine
both parts of the proof at once. But be careful: you must make sure that
the
proof reads correctly both from the top down and from the bottom up! (We
could not have done this with the previous proof: two different methods were
used.)
Second Note: If x 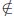 A ∪
B, what does that mean? Well, for x ∈ A ∪ B means
A ∪
B, what does that mean? Well, for x ∈ A ∪ B means
x ∈ A or x ∈ B. Thus if x 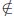 A ∪ B it must be
the case that
both x
A ∪ B it must be
the case that
both x 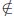 A and
A and
x 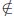 B.
B.
Definition: Let A1,A2, ..,An be a
collection of n sets. The union of A1,A2, ...,An
is the set A1 ∪A2 ∪...∪An = {x : x ∈ Ai
for some i ∈ {1, 2, ...n}}. The
intersection
of A1,A2, ...,An is the set A1 ∩ A2
∩ ... ∩ An = {x : x ∈ Ai
for every i ∈ {1, 2, ...n}}.
The union is sometimes denoted 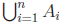 and the
intersection is sometimes denoted
and the
intersection is sometimes denoted
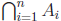 . Note: This should have all been covered in
your discrete math class (espe-
. Note: This should have all been covered in
your discrete math class (espe-
cially if you took that with me! ) If this is new to you, please come to see me
and
we will go over it.
Example: Let A1 = [0, 4),A2 = (−1, 6),A3
= [3, 5],A4 = [2,∞). Then A1 ∪ A2 ∪
A3
∪ A4 = (−1,∞) and A1 ∩ A2 ∩ A3 ∩ A4
= [3, 4).
Definition: Let A1,A2, ..,An be a
collection of n sets. The
product of A1,A2, ...,An
is the set 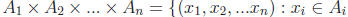 for every i ∈ {1, 2, ...n}}. The
for every i ∈ {1, 2, ...n}}. The
element 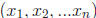 is called an ordered n-tuple. This
is sometimes denoted
is called an ordered n-tuple. This
is sometimes denoted
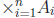 .
.
Example: A1 = {1, 2},A2 = {2, 3},A3 =
{4}. Then
A1 × A2 × A3 = {(1, 2, 4), (1, 3, 4), (2, 2,
4), (2, 3, 4)}.
Example: Note that R3= R × R × R.
Now we generalize to any union of any collection of sets and to any intersection
of
any collection of sets. Let = {1, 2, ..., n}. We could rewrite the union above
as
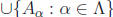 . But we can also understand
. But we can also understand
![]() to be any set, not
just a finite set:
to be any set, not
just a finite set:
Let ![]() be a nonempty
set. If for each α ∈
be a nonempty
set. If for each α ∈![]() there is a set Aα , the collection
there is a set Aα , the collection
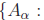
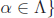 is called an indexed collection of
sets.
is called an indexed collection of
sets.
Example: Let 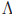 = R and for each α ∈
= R and for each α ∈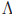 let Aα = [ α, α + 1). Then {Aα : α ∈
let Aα = [ α, α + 1). Then {Aα : α ∈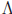 } is
} is
an indexed collection of sets. Note that A1 = [1, 2),A0 =
[0, 1),Aπ = [ π, π+ 1) etc.
Definition: Now we can define 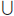 {Aα
: α ∈
{Aα
: α ∈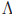 } = {x : x ∈ Aα for some α ∈
} = {x : x ∈ Aα for some α ∈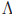 } and
} and
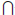 {Aα : α∈
{Aα : α∈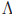 } = {x : x ∈Aα for every α ∈
} = {x : x ∈Aα for every α ∈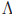 }.
}.
Examples:
1. Let ![]() =
=
![]() and for each α ∈
and for each α ∈![]() let Aα = [0, 1 +α ). Then
let Aα = [0, 1 +α ). Then
![]() {Aα } =
[0, 1]
{Aα } =
[0, 1]
and ![]() {Aα }
= [0,∞).
{Aα }
= [0,∞).
2. Let = 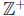 and for each
α ∈
and for each
α ∈![]() let Bα
= (−α , α). Then
let Bα
= (−α , α). Then ![]() {Bα
} = (−1, 1)
{Bα
} = (−1, 1)
and ![]() {Bα }
= R.
{Bα }
= R.
3. Let = Z and for each α ∈![]() let Dα = [ α, α+ 1]. Then
let Dα = [ α, α+ 1]. Then ![]() {Dα } =
{Dα } = 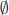 and
and
![]() {Dα } = R.
{Dα } = R.
Theorem (DeMorgan’s Law for Indexed Sets): Let {Aα : α ∈![]() } be an indexed
} be an indexed
collection of subsets of a set X. Then 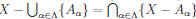 .
.
Proof: Let x ∈ X.
Then x ∈ X −
![]() {Aα }
{Aα } 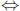
x 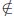
![]() {Aα }
{Aα } 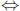
x 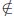 Aα for each and every α ∈
Aα for each and every α ∈![]()
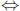
x ∈ X − Aα for every α ∈![]()
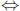
x ∈![]() {X − Aα
}. QED.
{X − Aα
}. QED.
Note: How can x not be in a union? If it is not in each and every one of the
sets!
That is how we proceed from the second to the third line in the proof above.
Second Note: To show that these two sets are equal we are actually using
the defi-
nition of set equality, showing that each set is a subset of the other, by
showing that
every element in one set is also an element of the other. (Go back and see how
we are
using the definitions if this is not clear to you. Or, come and see me! Sense a
theme
yet? )
Theorem (DeMorgan's Law for Indexed Sets): Let {Aα : α ∈![]() } be an indexed
} be an indexed
collection of subsets of a set X. Then 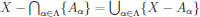 .
.
Proof: This proof is similar to the proof of DeMorgan's other law, given
above. Make
sure that you understand the reasoning behind it!
Theorem: Let {Aα : α ∈![]() } be an indexed collection of sets and let B be a set.
} be an indexed collection of sets and let B be a set.
Then B ∩ ![]() {Aα
} =
{Aα
} =
![]() {B ∩ Aα }.
{B ∩ Aα }.
Proof: Remember, to show that two sets are equal, we have to show that
each is a
subset of the other. This time, we cannot do this using a string of  s,
as the logic
s,
as the logic
doesn’t quite work both ways.
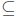 : Assume x ∈ B ∩
: Assume x ∈ B ∩
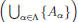 . Then x ∈ B and x ∈
. Then x ∈ B and x ∈
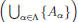 . Therefore there
. Therefore there
exists β ∈![]() such that x ∈ Aβ . Hence x ∈ B∩Aβ . It follows that
such that x ∈ Aβ . Hence x ∈ B∩Aβ . It follows that
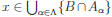 .
.
Thus we have B ∩ 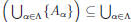 {B ∩ Aα }.
{B ∩ Aα }.
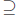 : Homework.
: Homework.
Theorem: Let {Aα : α ∈![]() } be an indexed collection of sets and let B be a set.
} be an indexed collection of sets and let B be a set.
Then B ∪ 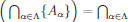 {B ∪ Aα }
{B ∪ Aα }
Proof:
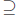 : Assume x ∈
: Assume x ∈![]() {B ∪Aα }. Then x ∈ B ∪Aα for every α ∈
{B ∪Aα }. Then x ∈ B ∪Aα for every α ∈![]() . Now either x ∈ B
. Now either x ∈ B
or x 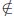 B.
B.
• If x ∈ B, then obviously x ∈ B ∪![]() .
.
• If x 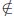 B, then since x ∈ B∪A for every
α ∈
B, then since x ∈ B∪A for every
α ∈![]() , it follows that
x ∈ Aα for every
, it follows that
x ∈ Aα for every
α ∈![]() . Therefore x ∈
. Therefore x ∈![]() {Aα } which implies that x ∈B∩
{Aα } which implies that x ∈B∩
![]() .
.
In either case we have x ∈ B ∪
![]() . This proves that
. This proves that 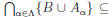
B ∪ ![]()
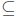 : Homework.
: Homework.

