Graphing Linear Equations
By the end of this section, you should be able to solve
the following problems:
1. Find the missing values in each coordinate pair and graph the equation
{(?, 2), (4, ?), (?, 0)}
2x + 3y = 2
2. Find the intercepts of the given equation.
−4x + 3y = 12
3. Graph the linear equation. Use intercepts where convenient.
2x − 3y = 1
4. Graph the linear equation. Use intercepts where
convenient.
−x + 2y = 4
2 Concepts
When we graph a linear equation we always get a line. That
means that it
certainly should not be curved in any way, nor should it have any “elbow”
joints in it. In our first example, we find three points and graph the line.
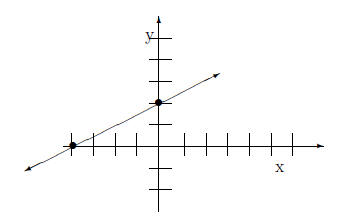
2.1 Example
Graph:
4x − 2y = 8.
for the values:
{(1, ?), (?, 2), (2, ?)}
In this example, we are given 2 values for x and one value
for y, and our
job is to find the missing values.
We substitute into the equation to find the missing value.
We begin with
x = 1.
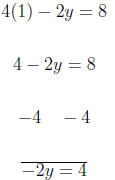
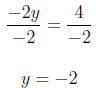
For y = 2 we have
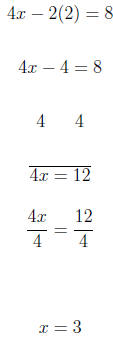
For x = 2 we have
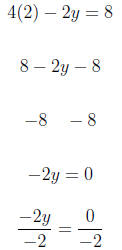
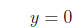
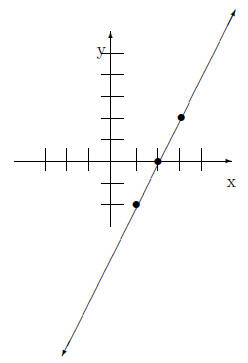
So the set of points we have to graph are: {(1,−2), (3,
2), (2, 0)}
Below we have plotted the points and drawn the graph:
3 Concepts
In our next example, we use what are called the
x-intercept and y-intercept to
graph the equation. To find the x-intercept for any equation, simply replace
the y variable with zero. Similarity, to find the y-intercept, simply replace
the x-variable with zero. An example will illustrate.
3.1 Example
Use intercepts to graph the following equation.
2x − 3y = −6
To get one x-intercept we replace y with 0.
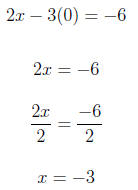
So the x-intercept is (-3,0). To find the y-intercept we
replace x with 0
in the equation.
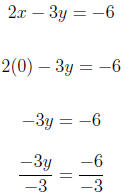
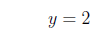
So the y-intercept is (0,2). The graph is below
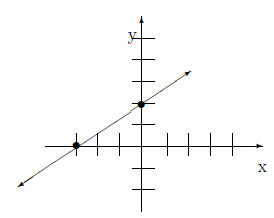
4 Facts
1. The equation of the y-axis is x = 0.
2. The equation of the x-axis is y = 0.
3. To find the x-intercept replace y with 0 in the equation and solve for x.
4. To find the y-intercept, replace x with zero in the equation and solve
for y.
5 Exercises
1. Find the missing value in each coordinate pair and graph the equation.
{( , 2), (4, ), ( , 0)}
2x + 3y = 2
2. Find the intercepts for the given equation.
−4x + 3y = 12
3. Graph the linear equation. Use intercepts where convenient.
2x − 3y = 1
4. Graph the linear equation. Use intercepts where convenient.
−x + 2y = 4
6 Solutions
1. Find the missing value in each coordinate pair and graph the equation.
{( , 2), (4, ), ( , 0)}
2x + 3y = 2
For y = 2 we have
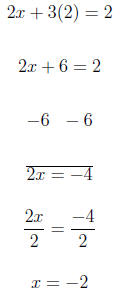
For x = 4
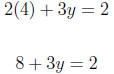
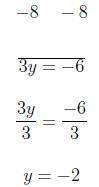
For y = 0
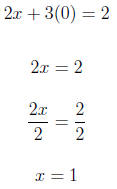
Therefore, we have:
{(−2, 2), (4,−2), (1, 0)}
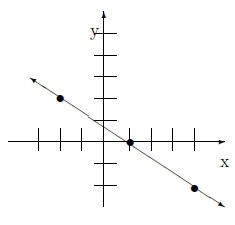
2. Find the intercepts for the given equation.
−4x + 3y = 12
For x = 0
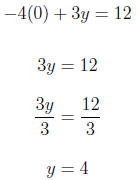
For y = 0
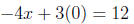
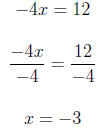
The intercepts are:
{(0, 4), (−3, 0)}
3. Graph the linear equation. Use intercepts where convenient.
2x − 3y = 1
We substitute in x = 2 so we get a number evenly divisible
by 3 on the
other side of the equation.
For x = 2
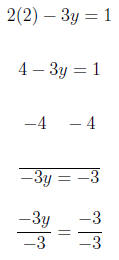
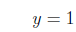
We substitute in y = 3 so we get a number evenly divisible
by 2 on the
other side of the equation. For y = 3
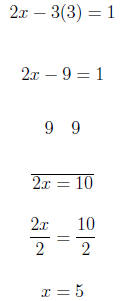
Using (2,1) and (5,3) we graph the equation.
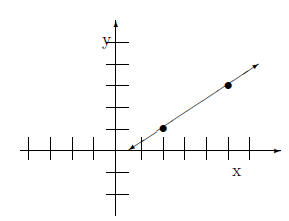
4. Graph the linear equation. Use intercepts where convenient.
−x + 2y = 4
For x = 0
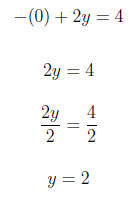
For y = 0
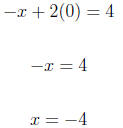
Using (0,2) and (-4,0) we graph the equation